Шифрование и криптоанализ

Введение

В современном мире остро стоит вопрос о конфиденциальности данных при обмене ими и их хранении, которая достигает за счет все возможных способов шифрования. Однако при появление новых алгоритмов шифрования начинают проводиться работы по изучению способов нарушить конфиденциальность данных, то есть ищут атаки на них.

В наше время широко распространены блочные алгоритмы шифрования, такие как AES, “Кузнечик” и др. Одним из потенциально эффективных способов проведения атак на них является линейный криптоанализ. Основную концепцию данного метода изложил Мицуру Мацуи (Mitsuru Matsui) в работе “Linear Cryptoanalysis Method for DES Cipher” в 90х годах. Суть данного метода будет изложена в данной статьи.

В качестве примера эффективного использования данного метода представлен криптоанализ блочного алгоритма шифрования NUSH , по которому будет приведена ниже.

Введение

Самая известная криптографическая проблема — передача секретных сообщений. Для этой задачи чаще всего используют криптосистемы с закрытым ключом: Алиса (отправитель) шифрует информацию с помощью ключа, а Боб (получатель) им же расшифровывает сообщение. К сожалению, криптосистемы с закрытым ключом имеют серьезные сложности в практической реализации. Основная вопрос — как раздать ключи? Во многих отношениях распределение ключей так же трудоемко, как и основная задача приватного общения. Злонамеренная третья сторона может подслушать ключ и легко прочитать сообщение.

Чтобы этого избежать, придумано множество способов, в этой статье мы рассмотрим квантовый, в котором секретность ключа гарантирована законами квантовой механики. Первая схема квантового распределения ключей (КРК) BB84 была разработана в 1984 году физиками Чарльзом Беннеттом и Жилем Брассаром. Ее основная идея состоит в том, чтобы использовать квантово- механический принцип (принцип неопределенности), согласно которому наблюдение в целом нарушает наблюдаемую систему. Таким образом, перехватчик, который подслушивает Алису и Боба, «портит» сообщение. Тогда его можно легко вычислить и выбросить «плохие» биты, а если их слишком много — начать все заново.

Введение

Криптоанализ — наука о том, как расшифровывать зашифрованную информацию, не имея в распоряжении ключа для расшифровки. Криптоанализом так же называется сам процесс дешифровки.

Чаще всего под криптоанализом понимается выяснение ключа шифрования, так как имея ключ криптоаналитик может расшифровать любое сообщение. Однако криптоанализ может заключаться и в анализе криптосистемы, а не только зашифрованного ею открытого сообщения, и включает также методы выявления уязвимости зашифровывающих алгоритмов.

Статистический криптоанализ — это один из методов криптоанализа. Как и в любой задаче, связанной с математической статистикой, вводится понятие статистики — некоторой величины, которая вычисляется на основе выборки или, в случае криптоанализа, — на основе криптограммы. В идеальном случае статистика должна быть простой в вычислении и использовании, а так же не сильно меняться от сообщения к сообщению, если эти сообщения зашифрованы одним и тем же ключом.

Цель статистического криптоанализа — расшифровать конечное сообщение, используя вычисленную статистику. В этой статье представлен обзор нескольких методов статистического криптоанализа от самых простых, до используемых в современных взломах.

Азы квантовой механики

Не будем вдаваться в подробности, а просто сформулируем основные утверждения. Начнем с принципа неопределенности. Он гласит, что некоторые физические величины вместе абсолютно точно не измеряются. Приведем в пример импульс и координату частицы: если поместить частицу в прибор точно измеряющий координату (например он показал ),а потом в прибор точно измеряющий импульс, то второй прибор выдаст случайное число(пусть это число , т.е.). Важный момент: раньше это была частица с координатой , теперь это частица с импульсом . Если ее поместить обратно в прибор измеряющий координату, он выдаст случайное число.

Теперь перейдем к поляризациям (нам неважно знать что это такое, будем считать ее просто физической величиной, характеризующей частицу). У одной поляризации есть два взаимно перпендикулярных направления, и зная какая поляризацию, мы можем эти направления определить

Пусть у нас есть две поляризации и (значками показано направление поляризации),у каждой соответственно по 2 состояния. Принцип неопределенности гласит, что не существует прибора, который смог бы различить все 4 состояния. Есть только два отдельных прибора, один различает состояния , второй . На этом факте и основан протокол BB84.

Задачи криптографии

Типичная схема обмена данными, к которым нельзя допускать посторонних, выглядит примерно так:

Абонент отправляет послание в открытом виде.
Инструменты криптографии зашифровывают информацию в сообщении.
Адресат выполняет расшифровку, задействовав ключ.

Только до25 декабря

Пройди опрос иполучи обновленный курс от Geekbrains

Дарим курс по digital-профессиям
и быстрому вхождения в IT-сферу

Чтобы получить подарок, заполните информацию в открывшемся окне

Перейти

Скачать файл

Можно сказать, что криптография – это особая тайнопись, защищающая информацию от мошенников.

Вот какие задачи выполняет криптография:

Передаваемая информация доступна лишь тем, у кого есть ключ. То есть, несанкционированный доступ исключен.
Подлинность сообщения (его источник всегда может быть проверена адресатом).
Целостность тоже можно проверить, то есть убедиться, что данные в ходе пересылки не претерпели изменений.
Отправка и пересылка гарантированы (ни одна из сторон не может отменить передачу).

Статистические атаки насыщения

Не только простейшие шифры подвержены статистическим методам криптоанализа. Например, статистические атаки насыщения направлены на блочные шифры, которые в настоящее время широко использутся в криптографических протоколах. Проиллюстрировать принцип таких атак удобно на блочном шифре PRESENT.

PRESENT

PRESENT — блочный шифр на основе SP-сети с размером блока 64 бита, длиной ключа 80 или 128 бит и количеством раундов 32. Каждый раунд состоит в операции XOR с текущим ключом, далее происходит рассеивание — пропускание через S-блоки, а затем полученные блоки перемешиваются.

Предложенная атака основывается на уязвимости шифра на этапе перемешивания. Как показано на изображении, из входных битов 5, 6, 9 и 10 s-блоков половина соединений идет в те же самые биты. И это только один пример подобной слабости. Значит, фиксируя 16 битов на входе 5, 6, 9 и 10 s-блоков, можно определить 8 входных битов для этих блоков на следующем раунде.

Предполагая ключ на данном шаге, криптоаналитик может по выбранном распределению выбранных 8 битов на входе определить распределение тех же 8 битов на выходе. Проделав эту процедуру для каждого ключа, можно понять все возможные распределения выбранных 8 выходных битов 5, 6, 9 и 10 s-блоков на каждом слое, применяя алгоритм итеративно.

Когда криптоаналитик знает для каждого ключа, как распределены выбранные 8 битов на каждом слое, он может сравнить полученные распределения с теми, которые получаются в реальной системе. Для этого нужен доступ к алгоритму шифрования и большое количество текстов для шифрования. Из всех возможных ключей выбирается тот, который минимизирует расстояние между теоретическим и экспериментальным распределениями.

Частотный анализ

Простые шифры

Частотный анализ использует гипотезу о том, что символы или последовательности символов в тексте имеют некоторое вероятностное распределение, которое сохраняется при шифровании и дешифровании.

Этот метод один из самых простых и позволяет атаковать шифры простой замены, в которых символы в сообщении заменяются на другие согласно некоторому простому правилу соответствия.

Однако такой метод совершенно не работает, например, на шифрах перестановки. В них буквы или последовательности в сообщении просто меняются местами, но их количество всегда остается постоянным, как в анаграммах, поэтому ломаются все методы, основанные на вычислении частот появления символов.

Для полиалфавитных шифров — шифров, в которых циклически применяются простые шифры замены — подсчет символов так же не будет эффективен, поскольку для кодировки каждого символа используется разный алфавит. Число алфавитов и их распределение так же неизвестно.

Шифр Виженера

Один из наиболее известных примеров полиалфавитных шифров — шифр Виженера. Он довольно прост в понимании и построении, однако после его создания еще 300 лет не находилось способа взлома этого шифра.

Пусть исходный текст это: МИНДАЛЬВАНГОГ

Составляется таблица шифров Цезаря по числу букв в используемом алфавите. Так, в русском алфавите 33 буквы. Значит, таблица Виженера (квадрат Виженера) будет размером 33х33, каждая i-ая строчка в ней будет представлять собой алфавит, смещенный на i символов.
Выбирается ключевое слово. Например, МАСЛО. Символы в ключевом слове повторяются, пока длина не достигнет длины шифруемого текста: МАСЛОМАСЛОМАС.
Символы зашифрованного текста определяются по квадрату Виженера: столбец соответствует символу в исходном тексте, а строка — символу в ключе. Зашифрованное сообщение: ЩЙЯРПШЭФМЬРПХ.

Этот шифр действительно труднее взломать, однако выделяющиеся особенности у него все же есть. На выходе все же не получается добиться равномерного распределения символов (чего хотелось бы в идеале), а значит потенциальный злоумышленник может найти взаимосвязь между зашифрованным сообщением и ключом. Главная проблема в шифре Виженера — это повторение ключа.

Взлом этого шифра разбивается на два этапа:

Поиск длины ключа. Постепенно берутся различные образцы из текста: сначала сам текст, потом текст из каждой второй буквы, потом из каждой третьей и так далее. В некоторый момент можно будет отвергнуть гипотезу о равномерном распределении букв в таком тексте — тогда длина ключа считается найденной.
Взлом нескольких шифров Цезаря, которые уже легко взламываются.

Поиск длины ключа — самая нетривиальная здесь часть. Введем индекс совпадений сообщения m:

где n — количество символов в алфавите и

p_i — частота появления i-го символа в сообщении. Эмпирически были найдены индексы совпадений для текстов на разных языков. Оказывается, что индекс совпадений для абсолютно случайного текста гораздо ниже, чем для осмысленного текста. С помощью этой эвристики и находится длина ключа.

Другой вариант — применить критерий хи-квадрат для проверки гипотезы о распределении букв в сообщении. Тексты, получаемые выкидыванием некоторых символов, все равно остаются выборкой из соответствующего распределения. Тогда в критерии хи-квадрат вероятности появления символов можно выбрать используя частотные таблицы языка.

IDEA

IDEA (International Data Encryption Algorithm) — алгоритм блочного симметричного шифрования, который был предложен на замену стандарта DES. Начальная версия алгоритма IDEA появилась в 1990 году. Алгоритм запатентован в США и в большинстве европейских стран. Владеет патентом Ascom Tech, но в некоммерческих целях алгоритм можно использовать бесплатно.

Размер блока в этом шифре — 64 бита, длина ключа — 128. Стоит сразу сказать, что алгоритм IDEA — самый молодой из перечисленных и его математика очень сложна. Минутка криптографического словарика.

Конфузия — шифрование должно зависеть от ключа сложным и запутанным способом.Диффузия — каждый бит незашифрованного текста должен влиять на каждый бит зашифрованного текста. Распространение одного незашифрованного бита на большое количество зашифрованных битов скрывает статистическую структуру незашифрованного текста.

В IDEA эти свойства достигаются за счет применения независимых математических операций. В отличие от DES, главной операцией которого является XOR (сложение по модулю 2), IDEA предусматривает наличие:

XOR;
сложения по модулю 216;
умножения по модулю (216 + 1).

Комбинирование этих трех операций обеспечивает комплексное преобразование входных данных, затрудняя криптоанализ IDEA по сравнению с DES.

В шифре IDEA выполняется восемь раундов, и в каждом раунде блок открытого текста подвергается преобразованию посредством математических операций. Любители «зреть в корень» могут позреть на схему одного раунда шифра IDEA, приведенную ниже. Блок текста, длиной 64 бита, делится на подблоки по 16 бит. Каждый такой полученный блочок поступает на вход раунда и подвергается сложному преобразованию.

Twofish

За первой рыбой появились еще две — новый алгоритм Twofish был разработан Шнайером и компанией для участия в конкурсе AES. Работа Шнайера вышла в пятерку финалистов, однако победителем так и не стала, хотя обладала для этого всеми возможными плюсами. Это:

128-битный блочный симметричный шифр;
длина ключей 128, 192 и 256 бит;
эффективная программная (в первую очередь на 32-битных процессорах) и аппаратная реализация;
гибкость (возможность использования ключа большей длины, применимость для поточного шифрования, хеш-функций и так далее);
простота алгоритма — его удобно анализировать.

Однако по сравнению с Rijndael, занявшим пьедестал AES, Twofish был более сложным для анализа и обладал более низкой скоростью шифрования. Разработан этот алгоритм на основе Blowfish с некоторыми дополнениями и также представляет собой сеть Фейстеля.
На конкурсе шифр подвергли различным типам криптоанализа. По сравнению с остальными финалистами конкурса AES он оказался самым стойким. Однако его необычное строение и относительная сложность породили некоторые сомнения в качестве этой прочности. На данный момент Twofish используется еще реже, чем его предшественник.

Операция «Раздолбай»

На главную
Задачи в Корявове
Лекции
Гуманитарные курсы
Английский язык
▼ 1 семестр
Аналитическая геометрия
Общая физика
Мат.Анализ (+коллоквиум)
История
▼ 2 семестр
Линейная алгебра
Мат.Анализ
Общая физика
▼ 3 семестр
Мат.Анализ
Лабы по общ.физу
Общая физика
Теоретическая механика
▼ 4 семестр
Мат.Анализ
Лабы по общ.физу
Общая физика
Дифф. уравнения
Теоретическая механика
▼ 5 семестр
Компьютерные сети
Теоретическая физика
ТФКП
Общая физика (ГОС)
▼ 6 семестр
Уравнения мат.физики
Мат.Анализ (ГОС)
▼ 7 семестр
Защита информации
Теоретическая физика
▼ 8 семестр
▼ 9+ семестры
Испанский язык
Философия (асп)

Моноалфавитный шифр

Моноалфавитный шифр — это, когда для шифрования используется одно отображение входного алфавита в выходной алфавит.

Криптоанализ

Для криптоаналитика существует следующая линия атаки. Если криптоаналитик имеет представление о природе открытого текста (например, о том что это несжатый текст на английском языке), то можно использовать известную информацию о характерных признаках, присущих текстам на соответствующем языке. Например, частотный криптоанализ, то есть определить относительную частоту появления в тексте различных букв и сравнить их со среднестатистическими данными для букв данного языка. Далее подход заключается в продолжении поиска характерных закономерностей (например известно, что обязательно присутствую некоторые слова). Один из очень эффективных методов заключается в подсчете частот биграмм и триграмм, комбинаций из двух и трех букв соответственно.

Среди моноалфавитных шифров существует омофонический шифр замены, где каждый символ открытого текста заменяется на несколько шифрозамен, причем каждая шифрозамена данного символа обозначает только этот символ. Такой шифр криптографически стойкий к частотному анализу, но он поддается анализу биграмм, триграмм и т.д.

Полиалфавитный шифр

Полиалфавитный шифр задает множество вариантов отображения входного алфавита на выходной алфавит — символы открытого теста заменяются разными функциями.

Шифрование

Исходный открытый текст разбивается на последовательные группы определенной длины — , где — период, выбираемый криптографом и держащийся секрете. Для удобства объяснений сообщение переписывается в виде матрицы, строками которой являются последовательные группы. Далее криптограф выбирает для каждого столбца свой моноалфавитный шифр.

Расшифровка

Легальный получатель знает период, разделяет принятую информацию по строкам и записывает в матрицу, к каждому столбцу применяет соответствующий ключ и расшифровывает сообщение.

Криптоанализ

Криптоаналитик должен сначала определить период, преобразовать шифрограмму в матрицу для предполагаемого периода и использовать для каждого столбца методы криптоанализа моноалфавитных шифров. При неудаче следует изменить предполагаемый период. Для нахождения периода чаще всего применяются:

метод Касиски,
автокорреляционный метод,
метод индекса совпадений.

Метод Касиски

Метод Касиски состоит в том, что в шифротексте осуществляется поиск одинаковых сегментов длин не меньше 3 и вычисляются расстояния между началами последовательных сегментов. Далее находится наибольший общий делитель (НОД) этих расстояний. Предполагаемый период является кратным этого делителя.

Автокорреляционный метод

Автокорреляционный метод состоит в том, что исходный шифротекст выписывается в строку, а под ней выписываются строки полученные сдвигом вправо на позиций. Для каждого подсчитывается число индексов таких, что . Вычисляются автокорреляционные коэффициенты .

Для чисел , кратных периоду , коэффициенты должны быть заметно больше, чем для сдвигов, не кратных периоду.

Метод индекса совпадений

Для последовательности из букв алфавита из букв индексом совпадения называется вероятность того, что два случайных элемента этой последовательности совпадают. Экспериментально индекс совпадений приближенно равен

где число появлений буквы в последовательности .
Период можно определить по формуле

где , — частота появления буквы в естественном языке.

Режимы работы шифров

ГОСТ 34.13-2018 содержит описание следующих режимов работы блочных шифров.

Режим простой замены

При зашифровании сообщение делится на блоки равной заданной длины. В случае, когда размер сообщения не кратен размеру блока, последний блок дополняется до нужной длины. Каждый блок независимо от остальных шифруется функцией, выполняющей блочное шифрования с использованием ключа.

Расшифрование происходит аналогичным образом. Причем если при зашифровании было применено дополнение, то при расшифровании применяется обратная операция.

Режим гаммирования

В данном режиме работы при шифровании каждый блок открытого текста складывается с блоком гаммы путем операции побитового сложения по модулю 2, XOR. Под гаммой понимается зашифрованная с использованием ключа последовательность, которую вырабатывает определенный алгоритм, который принимает на вход вектор инициализации.

Схематично изобразим данный режим при зашифровании и расшифровании, они происходят аналогично друг другу.

Если общая длина гаммы не кратна длине блока, то последний блок гаммы усекается до размера блока. Блоки гаммы отличны друг от друга и имеют псевдослучайных характер.

Режимы гаммирования с обратной связью: по выходу, по шифротексту

Два режима помещены в один пункт, так как они похожи между собой. В данных режимах при зашифровании выходные данные процедуры шифрования, либо сам шифротекст в случае обратной связи по шифротексту, подаются на вход следующей процедуре шифрования и так далее.

Отличие режимов можно увидеть на схеме.

При расшифровании схема преобразуется следующим образом. Шифротекст встает на место открытого текста, процедура шифрования сменяется процедурой расшифрования, а выходом алгоритма является расшифрованный текст. В дальнейших схемах будем это учитывать.

Режим простой замены с зацеплением

Особенностью данного режима работы является то, что каждый блок открытого текста, за исключением первого, складывается с предыдущим результатом шифрования.

Режим выработки имитовставки

При работе в данном режиме создается зависящий от всего текста блок, который предназначен для проверки наличия в шифротексте искажений.

Каждый из стандартов действителен с 1 июня 2019 года в соответствии с приказом Федерального агентства по техническому регулированию и метрологии. Актуальные ГОСТы наследуют разработки, прописанные в предыдущих версиях.

Режим гаммирования

Недостатков режима простой замены этот режим не имеет. Режим гаммирования называется так потому, что в нем используется гамма — псевдослучайная последовательность, которая в каждом раунде складывается по модулю 2 с открытым текстом. Гамма образуется из синхропосылки S — псевдослучайной последовательности, которая изменяется с каждой итерацией и проходит шифрование в режиме простой замены, после чего превращается в гамму и накладывается на открытый текст.

А теперь все по порядку.

Итак, пусть у нас есть синхропосылка S — 64-битная псевдослучайная последовательность.
S прошла через режим простой замены, при этом разбившись на два подблока — S и S₁.
Подблоки складываются с фиксированными константами:
S = S + Cmod232
S₁ = S₁ + C₁ — 1mod(232-1) + 1
Подблоки S и S₁ снова проходят режим простой замены, сращиваются, и получается результирующая гамма .
Открытый текст складывается по модулю 2 с полученной гаммой.

Шаги 3–5 повторяются для каждого блока. Все эти манипуляции можно посмотреть на схеме.

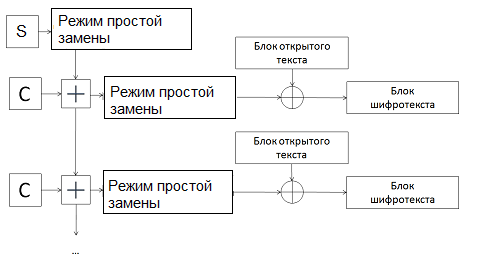Шифрование в режиме гаммирования

Расшифрование выполняется аналогично, вместо блока открытого текста подается блок шифротекста.

Частотный анализ

Простые шифры

Шифр Виженера

Пусть исходный текст это: МИНДАЛЬВАНГОГ

Составляется таблица шифров Цезаря по числу букв в используемом алфавите. Так, в русском алфавите 33 буквы. Значит, таблица Виженера (квадрат Виженера) будет размером 33х33, каждая i-ая строчка в ней будет представлять собой алфавит, смещенный на i символов.
Выбирается ключевое слово. Например, МАСЛО. Символы в ключевом слове повторяются, пока длина не достигнет длины шифруемого текста: МАСЛОМАСЛОМАС.
Символы зашифрованного текста определяются по квадрату Виженера: столбец соответствует символу в исходном тексте, а строка — символу в ключе. Зашифрованное сообщение: ЩЙЯРПШЭФМЬРПХ.

Взлом этого шифра разбивается на два этапа:

Поиск длины ключа. Постепенно берутся различные образцы из текста: сначала сам текст, потом текст из каждой второй буквы, потом из каждой третьей и так далее. В некоторый момент можно будет отвергнуть гипотезу о равномерном распределении букв в таком тексте — тогда длина ключа считается найденной.
Взлом нескольких шифров Цезаря, которые уже легко взламываются.

Поиск длины ключа — самая нетривиальная здесь часть. Введем индекс совпадений сообщения m:

где n — количество символов в алфавите и

Статистические атаки насыщения

PRESENT

Предложенная атака основывается на уязвимости шифра на этапе перемешивания. Как показано на изображении, из входных битов 5, 6, 9 и 10 s-блоков половина соединений идет в те же самые блоки. И это только один пример подобной слабости. Значит, фиксируя 16 битов на входе 5, 6, 9 и 10 s-блоков, можно определить 8 входных битов для этих блоков на следующем раунде.

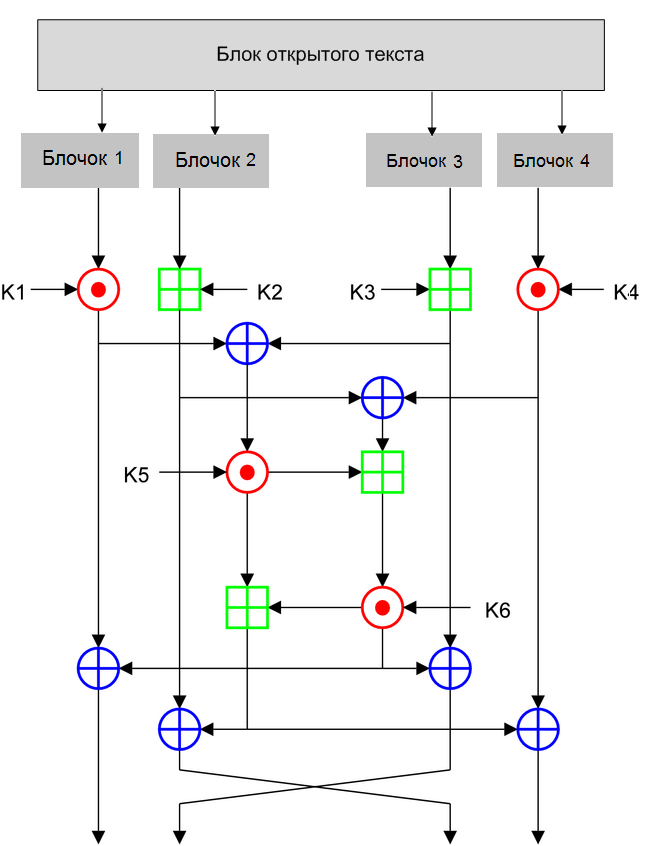
Режим простой замены

В режиме простой замены на 32 раунда, согласно стандарту, нам нужно 32 раундовых ключа. Для генерации раундовых ключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: . Ключи являются циклическим повторением ключей . Ключи являются ключами .

Каждый блок 64 бита делится на два подблока — A_i и B_i.
Левый подблок Ai складывается по модулю 232 с раундовым ключом K1: .
Левый подблок проходит через S-бокс.
Биты левого подблока сдвигаются на 11 позиций (циклический сдвиг).
Левый подблок складывается с правым по модулю 2: .
Правый подблок принимает первоначальное значение левого подблока: .
Подблоки меняются местами.

Сразу пример одного раунда. Ключ 256 бит:

Тогда раундовые ключи

Как пользоваться таким S-боксом? Очень просто! Если на входе S-бокса 0, то на выходе будет 1 (берем 0-й символ S-бокса), если 4, то на выходе будет 5 (берем 4-й символ), если на входе 7, то на выходе 4, и так далее.

Открытый текст:

Входной блок 64 бита

Делится на два 32-битных блока старших и младших битов:

Схема деления на блоки

Пример, конечно, вышел дикий, потому что ГОСТ — это все-таки не такой стандарт, чтоб каждый мог его ручками перебирать.

Режим простой замены чересчур простой и имеет существенные недостатки:

одна ошибка в шифрованном блоке искажает все биты этого блока;
при шифровании одинаковых блоков открытого текста получаются одинаковые блоки шифротекста, что может дать определенную информацию криптоаналитику.

Таким образом, применять ГОСТ 28147—89 в режиме простой замены желательно лишь для шифрования ключевых данных.

Протокол BB84

Выпишем наш словарь:

1) (индексом обозначен базис квантового состояния)

Алиса — передает; Боб — принимает; Ева — перехватывает

рис.1

На рисунке 1 показана схема передачи.

Действия Алисы

Действия Боба

Случайно выбирает базис и бит (0 или 1). Отправляет последовательность 0 и 1 в соответствующих базисах Бобу

Получает бит и, чтобы его расшифровать, случайно выбирает базис в котором будет измерять поляризацию. Если он угадал базис, то он получил верный бит, если нет, то он не знает никакой информации о переданном бите. Аналогично со следующими битами информации

После сеанса передачи Алиса и Боб созваниваются по открытому каналу. Далее Боб спрашивает у Алисы по каждому переданному биту правильно ли он выбрал базис (сам бит не называет). Если выбранные Бобом и Алисой базисы совпадают, то бит успешно передан, если нет, то отбрасывается. В процессе передачи данных, бит мог «испортится» (при применении верной поляризации получается неправильный бит). Это может произойти например из-за активной атаки Евы или же из-за особенностей квантового канала. При просмотре бита неверной поляризацией, его поляризация изменяется и невозможно вычислить его изначальное состояние. Для проверки количества ошибок Алиса и Боб раскрывают часть неверных битов. В протоколе BB84 критической величиной ошибок является 11% , это значит что Ева пыталась перехватить сообщение. В таком случае перепроверяют квантовый канал и начинают заново.

Рассмотрим возможные действия Евы. Она может пытаться перехватывать биты через квантовый канал: так же как Боб случайно выбирать поляризацию. Однако ей это не сильно поможет прочитать сообщение, она, в отличие от Боба, не может переговариваться с Алисой для выбора нужных позиций битов(вероятность, того что она будет выбирать ту же поляризацию, что и Боб крайне мала для длинных последовательностей). При, этом в случае неправильно угаданных поляризаций, она будет «портить» биты. Боб и Алиса будут знать: их сообщения пытаются перехватить. Теперь пусть Ева дополнительно активно атакует классический канал (активно, то есть не просто подслушивает, а еще может менять информацию). Тогда она может представиться Алисе Бобом, прочитать сообщение, а после стать Алисой для Боба и передать сообщение дальше. В таком случае Ева прочитает секретное сообщение, а Алиса и Боб ничего не заподозрят.

Из рассмотренного выше следует, что для надежности передачи информации нужно предъявить определенные требования к каналам связи:

1)Информацию из квантового канала можно менять, но нельзя подслушать.

2)Информацию из классического канала можно прослушивать, но ни в коем случае нельзя менять.