Нейроморфное будущее: попытка вложить мозг в сервер

Резюме

В данной статье мы познакомились со свёрточными сетями и рассмотрели основные используемые слои. Для большего удобства мы собрали всё самое главное в табличку:

Слой	Гиперпараметры	Размер входа	Размер выхода	Обучаемые параметры
Свёрточный	fc, fs, S, P	WxHxD	W — fs + 2P S +1 х H — fs + 2P S +1 х fc	fc·(fs·fs·fd + 1)
Пулинг	k	WxHxD	W k x H k x D
Активационный	—	WxHxD	WxHxD	≥ 0
Полносвязный	N	1x1xD	1x1xN	N·(D+1)

В следующих публикациях мы подробно расскажем, как вычисляются градиенты на каждом из слоёв, чтобы можно было построить свою первую свёрточную нейронную сеть с нуля и затем обучить её.

Следующая часть: Свёрточная нейронная сеть с нуля. Часть 1. Свёрточный слой

Нейронная сеть с «шипами»

Плотная сеть нейронов, соединенных синапсами на нейроморфном чипе, называется «шипованная нейронная сеть» (Spiking Neural Network). Нейроны взаимодействуют друг с другом, передавая импульсы через синапсы

Вышеупомянутые чипы реализуют эту сеть на аппаратном уровне, но огромное внимание уделяется ее моделированию в программном обеспечении, а также для оценки производительности или решения проблем распознавания образов и других прикладных задач машинного обучения

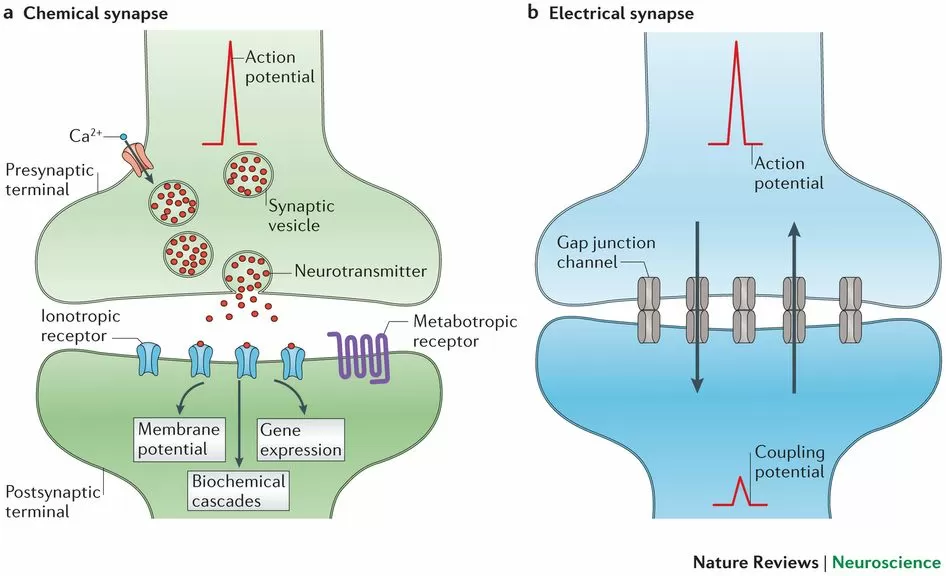
«Нейронные сети с шипами» кодируют информацию во временном домене в виде «поездов с шипами», т.е. разница во времени между двумя последовательными шипами определяет свойства сети. Функционирование самого основного элемента сети — нейрона, регулируется дифференциальным уравнением. Вход в нейрон осуществляется в виде дискретных шипов во временной области, а не в виде непрерывных значений. Благодаря этим идиосинкразиям, SNN методология, используемая для его обучения, также отличается от существующих искусственных нейронных сетей. Вместо градиентного спуска используется более биологически правдоподобное Хеббианское Обучение (Hebbian Learning). Оно также называется Spike Time Dependent Plasticity (STDP).

Поначалу все это может показаться эзотерическим и требует времени, чтобы понять сетевую динамику SNN. Поскольку эта технология все еще находится в стадии развития, имеющейся документации недостаточно для полного понимания.

Эта серия блогов направлена на развитие понимания SNN с нуля с каждым элементом сети, подробно объясненным и реализованным на Python. Также будут обсуждаться существующие на Python библиотеки для SNN.

Рон Амадео

11/02.2020

Линейная функция активации

A = cx

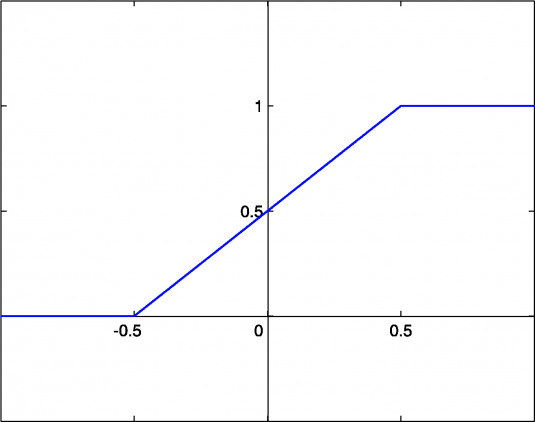
Линейная функция представляет собой прямую линию и пропорциональна входу (то есть взвешенной сумме на этом нейроне).

Такой выбор активационной функции позволяет получать спектр значений, а не только бинарный ответ. Можно соединить несколько нейронов вместе и, если более одного нейрона активировано, решение принимается на основе применения операции max (или softmax). Но и здесь не без проблем.

Если вы знакомы с методом градиентного спуска для обучения, то можете заметить, что для этой функции производная равна постоянной.

Производная от A=cx по x равна с. Это означает, что градиент никак не связан с Х. Градиент является постоянным вектором, а спуск производится по постоянному градиенту. Если производится ошибочное предсказание, то изменения, сделанные обратным распространением ошибки, тоже постоянны и не зависят от изменения на входе delta(x).

Это не есть хорошо (не всегда, но в большинстве случаев). Но существует и другая проблема. Рассмотрим связанные слои. Каждый слой активируется линейной функцией. Значение с этой функции идет в следующий слой в качестве входа, второй слой считает взвешенную сумму на своих входах и, в свою очередь, включает нейроны в зависимости от другой линейной активационной функции.

Не имеет значения, сколько слоев мы имеем. Если все они по своей природе линейные, то финальная функция активации в последнем слое будет просто линейной функцией от входов на первом слое! Остановитесь на мгновение и обдумайте эту мысль.

Это означает, что два слоя (или N слоев) могут быть заменены одним слоем. Мы потеряли возможность делать наборы из слоев

Не важно, как мы стэкаем, вся нейронная сеть все равно будет подобна одному слою с линейной функцией активации (комбинация линейных функций линейным образом — другая линейная функция)

Альтернативные технологии

Большие компании, а также ученые пытаются обойти эту проблему чтобы не оказаться на дне индустрии. Передовые группы разработчиков Intel предполагают, что компания будет адаптировать новые материалы и структуры транзисторов для большего контроля проходящего тока. С ростом популярности машинного обучения, а также разнообразных новых и сложных алгоритмов, требования к процессорам, которые смогли бы выполнять сложные вычисления, выросли.

Ученые по всему миру работают в таких областях:

Среди вышеперечисленных направлений квантовые вычисления и углеродные нанотрубки находятся на начальной стадии развития. Они до сих пор не способны на полную замену кремния, не говоря уже об их промышленном производстве. GPU используются уже давно, но они потребляют много энергии. Нейроморфное оборудование также находится на относительно промежуточных стадиях разработки, но обеспечивает весьма вероятное решение грядущего кризиса производительности.

Почему именно свёрточные сети?

Нам известно, что нейронные сети хороши в распознавании изображений. Причём хорошая точность достигается и обычными сетями прямого распространения, однако, когда речь заходит про обработку изображений с большим числом пикселей, то число параметров для нейронной сети многократно увеличивается. Причём настолько, что время, затрачиваемое на их обучение, становится невообразимо большим.

Так, если требуется работать с цветными изображениями размером 64х64, то для каждого нейрона первого слоя полносвязной сети потребуется 64·64·3 = 12288 параметров, а если сеть должна распознавать изображения 1000х1000, то входных параметров будет уже 3 млн! А помимо входного слоя есть и другие слои, на которых, зачастую, число нейронов превышает количество нейронов на входном слое, из-за чего 3 млн запросто превращаются в триллионы! Такое количество параметров просто невозможно рассчитать быстро ввиду недостаточно больших вычислительных мощностей компьютеров.

Главной особенностью свёрточных сетей является то, что они работают именно с изображениями, а потому можно выделить особенности, свойственные именно им. Многослойные персептроны работают с векторами, а потому для них нет никакой разницы, находятся ли какие-то точки рядом или на противоположных концах, так как все точки равнозначны и считаются совершенно одинаковым образом. Изображения же обладают локальной связностью. Например, если речь идёт об изображениях человеческих лиц, то вполне логично ожидать, что точки основных частей лица будут рядом, а не разрозненно располагаться на изображении. Поэтому требовалось найти более эффективные алгоритмы для работы с изображениями и ими оказались свёрточные сети.

Гиперболический тангенс

Еще одна часто используемая активационная функция — гиперболический тангенс.

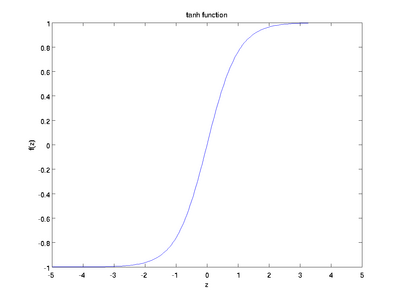
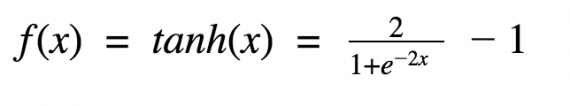
Гиперболический тангенс очень похож на сигмоиду. И действительно, это скорректированная сигмоидная функция.

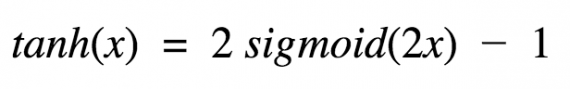
Поэтому такая функция имеет те же характеристики, что и у сигмоиды, рассмотренной ранее. Её природа нелинейна, она хорошо подходит для комбинации слоёв, а диапазон значений функции -(-1, 1). Поэтому нет смысла беспокоиться, что активационная функция перегрузится от больших значений. Однако стоит отметить, что градиент тангенциальной функции больше, чем у сигмоиды (производная круче). Решение о том, выбрать ли сигмоиду или тангенс, зависит от ваших требований к амплитуде градиента. Также как и сигмоиде, гиперболическому тангенсу свойственная проблема исчезновения градиента.

Тангенс также является очень популярной и используемой активационной функцией.

Слой подвыборки (пулинга)

Данный слой позволяет уменьшить пространство признаков, сохраняя наиболее важную информацию. Существует несколько разных версий слоя пулинга, среди которых максимальный пулинг, средний пулинг и пулинг суммы. Наиболее часто используется именно слой макспулинга.

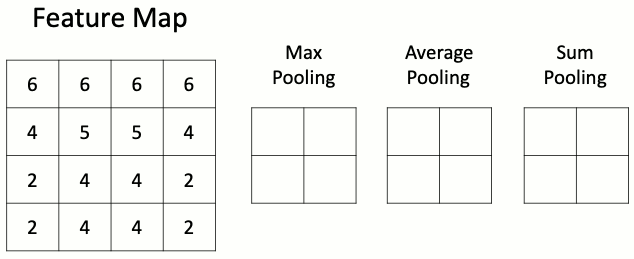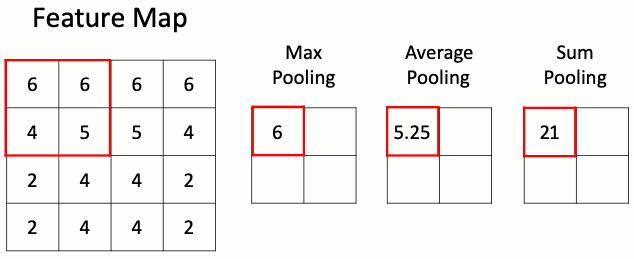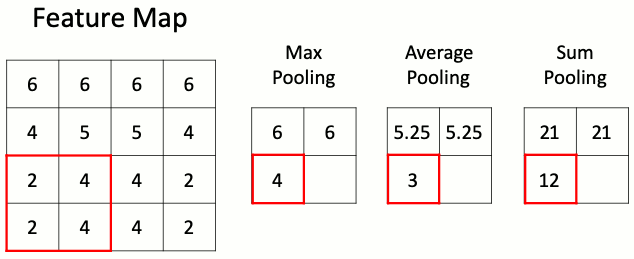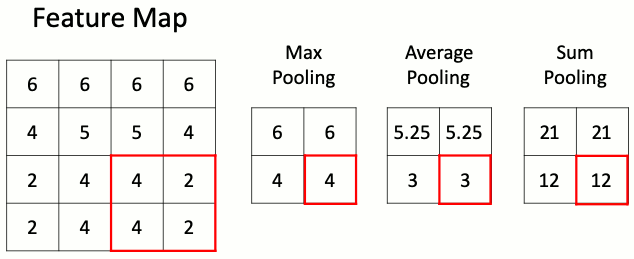
Слою подвыборки требуется всего один гиперпараметр — шаг пулинга, то есть число раз, в которое нужно сократить пространственные размерности. Наиболее часто используется слой макспулинга с уменьшением размера входного тензора в два раза. Некоторые библиотеки позволяют задавать раздельные параметры уменьшения по высоте и ширине, однако чаще всего эти параметры совпадают.

ReLu

Следующая в нашем списке — активационная функция ReLu,

A(x) = max(0,x)

Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и в противном случае. Схема работы приведена ниже.

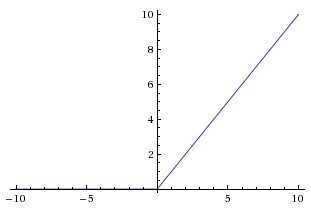
На первый взгляд кажется, что ReLu имеет все те же проблемы, что и линейная функция, так как ReLu линейна в первом квадранте. Но на самом деле, ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [0,inf), то есть активация может “взорваться”.

Следующий пункт — разреженность активации. Представим большую нейронную сеть с множеством нейронов. Использование сигмоиды или гиперболического тангенса будет влечь за собой активацию всех нейронов аналоговым способом. Это означает, что почти все активации должны быть обработаны для описания выхода сети. Другими словами, активация плотная, а это затратно. В идеале мы хотим, чтобы некоторые нейроны не были активированы, это сделало бы активации разреженными и эффективными.

ReLu позволяет это сделать. Представим сеть со случайно инициализированными весами (или нормализированными), в которой примерно 50% активаций равны из-за характеристик ReLu (возвращает для отрицательных значений х). В такой сети включается меньшее количество нейронов (разреженная активация), а сама сеть становится легче. Отлично, кажется, что ReLu подходит нам по всем параметрам. Но ничто не безупречно, в том числе и ReLu.

Из-за того, что часть ReLu представляет из себя горизонтальную линию (для отрицательных значений X), градиент на этой части равен . Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки.

ReLu менее требовательно к вычислительным ресурсам, чем гиперболический тангенс или сигмоида, так как производит более простые математические операции. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.

Ступенчатая функция активации

Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем.

• Функция А = активирована, если Y > граница, иначе нет.
• Другой способ:  A = 1, если Y > граница, иначе А = 0.

Функция, которую мы только что создали, называется ступенчатой. Такая функция представлена на рисунке ниже.

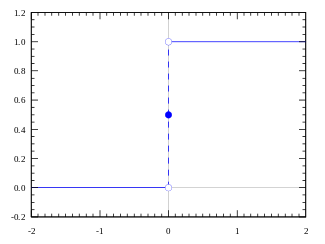
Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.

Мы создали активационную функцию для нейрона. Это простой способ, однако в нём есть недостатки. Рассмотрим следующую ситуацию.

Представим, что мы создаем бинарный классификатор — модель, которая должна говорить “да” или “нет” (активирован или нет). Ступенчатая функция сделает это за вас — она в точности выводит 1 или 0.

Теперь представим случай, когда требуется большее количество нейронов для классификации многих классов: класс1, класс2, класс3 и так далее. Что будет, если активированными окажутся больше чем 1 нейрон? Все нейроны из функции активации выведут 1. В таком случае появляются вопросы о том, какой класс должен в итоге получиться для заданного объекта.

Мы хотим, чтобы активировался только один нейрон, а функции активации других нейронов были равна нулю (только в этом случае можно быть уверенным, что сеть правильно определяет класс). Такую сеть труднее обучать и добиваться сходимости. Если активационная функция не бинарная, то возможны значения “активирован на 50%”, “активирован на 20%” и так далее. Если активированы несколько нейронов, можно найти нейрон с наибольшим значением активационной функции (лучше, конечно, чтобы это была softmax функция, а не max. Но пока не будем заниматься этими вопросами).

Но в таком случае, как и ранее, если более одного нейрона говорят “активирован на 100%”, проблема по прежнему остается. Так как существуют промежуточные значения на выходе нейрона, процесс обучения проходит более гладко и быстро, а вероятность появления нескольких полностью активированных нейронов во время тренировки снижается по сравнению со ступенчатой функцией активации (хотя это зависит от того, что вы обучаете и на каких данных).

Мы определились, что хотим получать промежуточные значения активационной функции (аналоговая функция), а не просто говорить “активирован” или нет (бинарная функция).

Первое, что приходит в голову — линейная функция.

Как выбрать функцию активации?

Настало время решить, какую из функций активации использовать. Следует ли для каждого случая использовать ReLu? Или сигмоиду? Или tanh? На эти вопросы нельзя дать однозначного ответа. Когда вы знаете некоторые характеристики функции, которую пытаетесь аппроксимировать, выбирайте активационную функцию, которая аппроксимирует искомую функцию лучше и ведет к более быстрому обучению.

Например, сигмоида хорошо показывает себя в задачах классификации (посмотрите еще раз на пункт про сигмоиду. Не присущи ли ей свойства идеального классификатора?), так как аппроксимацию классифицирующей функции комбинацией сигмоид можно провести легче, чем используя ReLu, например.

Используйте функцию, с которой процесс обучения и сходимость будут быстрее. Более того, вы можете использовать собственную кастомную функцию! Если вы не знаете природу исследуемой функции, в таком случае начните с ReLu и потом работайте в обратном направлении. В большинстве случаев ReLu работает как хороший аппроксиматор.

Что представляют свёрточные нейронные сети

В отличие от сетей прямого распространения, которые работают с данными в виде векторов, свёрточные сети работают с изображениями в виде тензоров. Тензоры — это 3D массивы чисел, или, проще говоря, массивы матриц чисел.

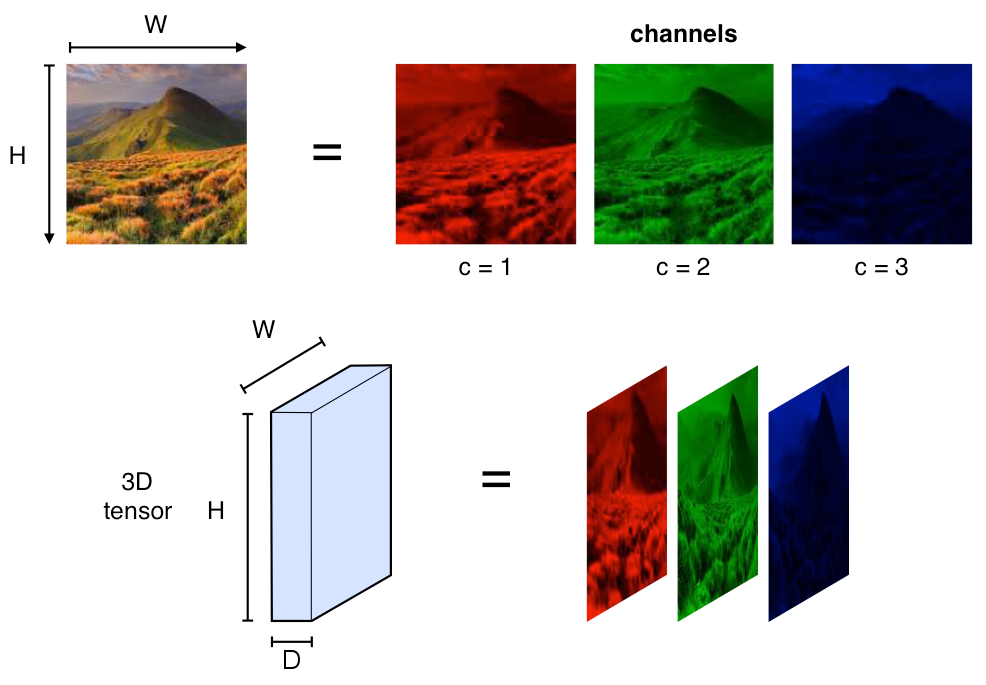
Представление изображений

Изображения в компьютере представляются в виде пикселей, а каждый пиксель – это значения интенсивности соответствующих каналов. При этом интенсивность каждого из каналов описывается целым числом от 0 до 255. Чаще всего используются цветные изображения, которые состоят из RGB пикселей – пикселей, содержащих яркости по трём каналам: красному, зелёному и синему. Различные комбинации этих цветов позволяют создать любой из цветов всего спектра. Именно поэтому вполне логично использовать именно тензоры для представления изображений: каждая матрица тензора отвечает за интенсивность своего канала, а совокупность всех матриц описывает всё изображение.

Изображение цифры из датасета MNIST

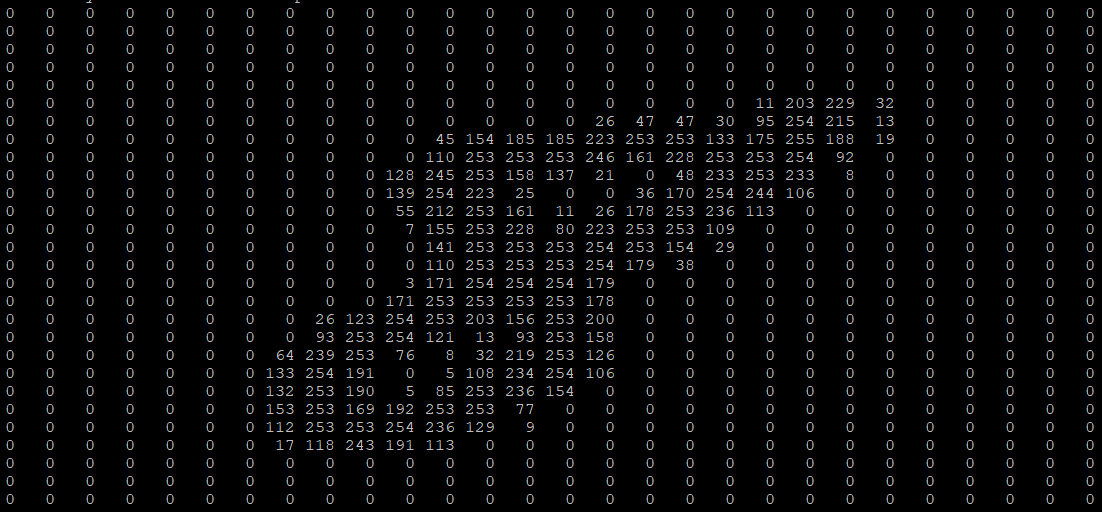
Эта же цифра в компьютере

Нейроморфное оборудование

Человеческий мозг является самой энергоэффективной и самой быстродейственной системой задержки, существующей на Земле. Он обрабатывает сложную информацию быстрее и гораздо лучше, чем любой компьютер. Во многом это связано с его архитектурой, которая состоит из плотных нейронов, эффективно передающих сигналы через свои синапсы. Целью нейроморфной инженерии является реализация этой архитектуры и производительности в кремнии. Термин был придуман Карвером Мидом в конце 1980-х годов, описывая системы, содержащие аналоговые/цифровые схемы, имитирующие нейробиологические элементы, присутствующие в нервной системе. Многие исследовательские учреждения инвестировали в разработку чипов, которые могут делать то же самое.

Нейроморфный чип IBM — TrueNorth имеет 4096 ядер, каждое из которых имеет 256 нейронов, и каждый нейрон имеет 256 синапсов для связи с другими. Архитектура, будучи очень близкой к мозгу, очень эффективна в аспекте энергопотребления. Аналогично, Loihi от Intel может похвастаться 128 ядрами, каждое ядро имеет 1024 нейрона. Группа APT из Университета Манчестера недавно обнаружила самый быстрый в мире суперкомпьютер — SpiNNaker, состоящий только из нейроморфных ядер. Brainchip — еще одна компания, разрабатывающая аналогичные чипы для приложений в области обработки данных, кибербезопасности и финансовых технологий. Проект The Human Brain Project — это масштабный проект, финансируемый Евросоюзом, который ищет ответ на вопрос – как создавать новые алгоритмы и компьютеры, имитирующие работу мозга.

Все эти системы имеют одну общую черту – все они отличаются высокой энергоэффективностью. TrueNorth потребляет 1/10,000 удельной мощности обычного процессора Джона фон Неймана. Эта гигантская разница обусловлена асинхронной природой обработки на чипе, как в человеческом мозге. Каждый нейрон не нуждается в обновлении на каждом шаге. Только те, которые находятся в действии, требуют энергии. Это называется событийно-ориентированной обработкой и является самым важным аспектом для визуализации нейроморфных систем как подходящей альтернативы для обычных архитектур.

Список литературы

1. Using neuro-accelerators on FPGAs in collaborative robotics tasks / A. Zelensky, E. Semenishchev, A. Alepko // SPIE Optical Instrument Science, Technology, and Applications II. — 2021. — Vol. 11876. – Art. 118760O. — Р. 5. https://doi.org/10.1117/12.2600582

2. Zelenskii, A. A. Control of Collaborative Robot Systems and Flexible Production Cells on the Basis of Deep Learning / A. A. Zelenskii, M. M. Pismenskova, V. V. Voronin // Russian Engineering Research. — 2019. — Vol. 39. — P. 1065–1068. https://doi.org/10.3103/S1068798X19120256

3. Automated visual inspection of fabric image using deep learning approach for defect detection / V. V. Voronin, R. A. Sizyakin, M. Zhdanova // Automated Visual Inspection and Machine Vision IV. — 2021. — Vol. 11787. — P. 117870. https://doi.org/10.1117/12.2592872

4. NeuFlow: Dataflow Vision Processing System-on-a-Chip / Phi-Hung Pham, D. Jelaca, C. Farabet // In: Proc. IEEE 55th International Midwest Symposium on Circuits and Systems (MWSCAS). — 2012. — P. 1044-1047. https://doi.org/10.1109/MWSCAS.2012.6292202

5. Шуремов, Е. Л. Стоит ли увлекаться Большими Данными? / Е. Л. Шуремов // Учет. Анализ. Аудит. — 2020. — Т. 7, № 2. — С.17–29. https://doi.org/10.26794/2408-9303-2020-7-2-17-29

6. Towards artificial general intelligence with hybrid Tianjic chip architecture / Jing Pei, Lei Deng, Sen Song // Nature. — 2019. — Vol. 572. — P. 106–111. https://doi.org/10.1038/s41586-019-1424-8

7. Модха, Д. TrueNorth: от нуля к 64 миллионам нейронов / Д. Модха // Открытые системы. СУБД. 2019. — № 3. — С. 8.

8. TrueNorth: design and tool flow of a 65 mw 1 million neuron programmable neurosynaptic chip / F. Akopyan, J. Sawada, A. Cassidy // IEEE transactions on computer-aided design of integrated circuits and systems. — 2015. — Vol. 34. — P. 1537–1557. https://doi.org/10.1109/TCAD.2015.2474396

9. Loihi: A neuromorphic manycore processor with on-chip learning / Mike Davies, Narayan Srinivasa, Tsung-Han Lin // IEEE Micro. — 2018. — Vol. 38. — P. 82–99. https://doi.org/10.1109/MM.2018.112130359

10. Efficient synapse memory structure for reconfigurable digital neuromorphic hardware / J. Kim, J. Koo, T. Kim, J. J. Kim // Frontiers in neuroscience. — 2018. — Vol. 12. — P. 829. https://doi.org/10.3389/fnins.2018.00829

11. Федоров, А. Квантовые вычисления: от науки к приложениям / А. Федоров // Открытые системы. СУБД. — 2019. — № 3. — С. 14.

12. What Happens When ‘If’ Turns to ‘When’ in Quantum Computing? / J. F. Bobier, M. Langione, E. Tao // BCG Digital Transformation. — 2021. — P. 20.

13. Сабанов, А. Г. Доверенные системы как средство противодействия киберугрозам / А. Г. Сабанов // Защита информации. Инсайд. — 2015. — № 3 (63). — С. 17–21.

14. Каляев, И. А. Доверенные системы управления / И. А. Каляев, Э. В. Мельник // Мехатроника, автоматизация, управление. — 2021. — Т. 22, № 5. — С. 227–236. https://doi.org/10.17587/mau.22.227-236

Свёрточный слой

Слой свёртки, как можно догадаться по названию типа нейронной сети, является самым главным слоем сети. Его основное назначение – выделить признаки на входном изображении и сформировать карту признаков. Карта признаков – это всего лишь очередной тензор (массив матриц), в котором каждый канал отвечает за какой-нибудь выделенный признак.

Для того, чтобы слой мог выделять признаки, в нём имеются так называемые фильтры (или ядра). Ядра — это всего лишь набор тензоров. Эти тензоры имеют один и тот же размер, а их количество определяет глубину выходного 3D массива. При этом глубина самих фильтров совпадает с количеством каналов входного изображения. Так, если на вход свёрточному слою подаётся RGB изображение и требуется карта признаков, состоящая из 32 каналов, то свёрточный слой будет содержать в себе 32 фильтра глубиной 3.

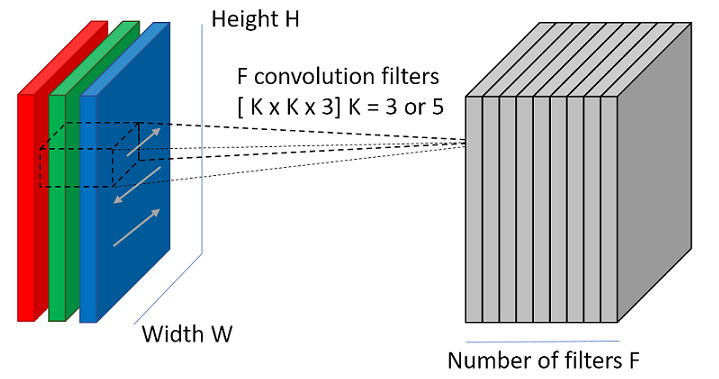
Для того, чтобы сформировать карту признаков из входного изображения, производится операция свёртки входного тензора с каждым из фильтров. Свёртка – это операция вычисления нового значения выбранного пикселя, учитывающая значения окружающих его пикселей. Алгоритм получения результата свёртки можно описать так:

Фильтр накладывается на левую верхнюю часть изображения и производится покомпонентное умножение значений фильтра и значений изображения, после чего фильтр перемещается дальше по изображению до тех пор, пока аналогичным образом не будут обработаны все его участки.

Затем числа полученных матриц суммируются в единую матрицу — результат применения фильтра.

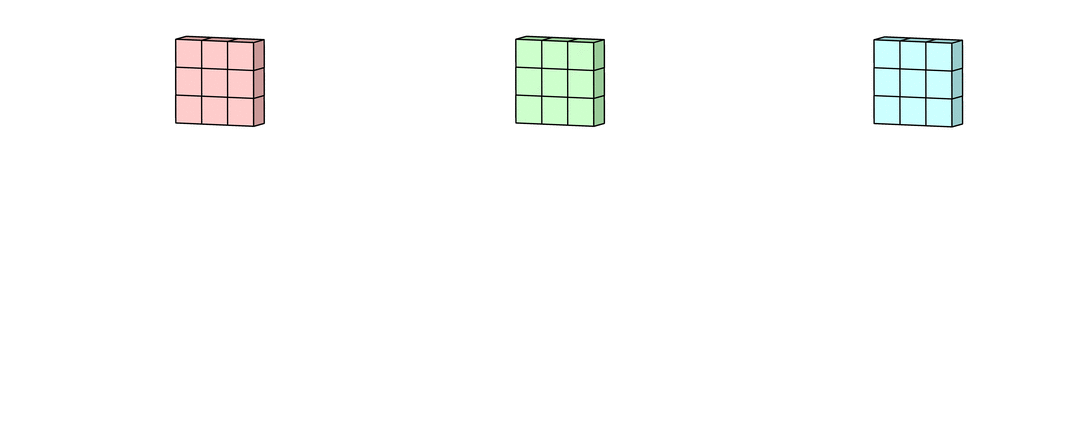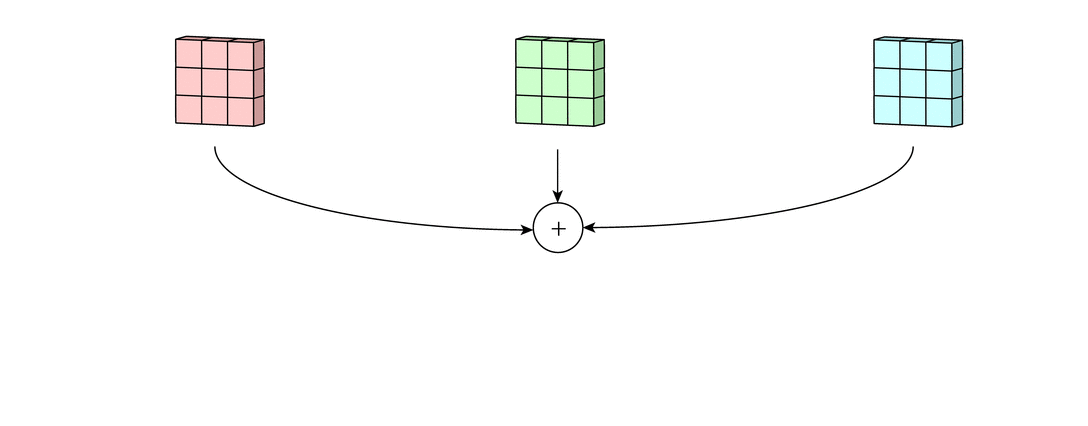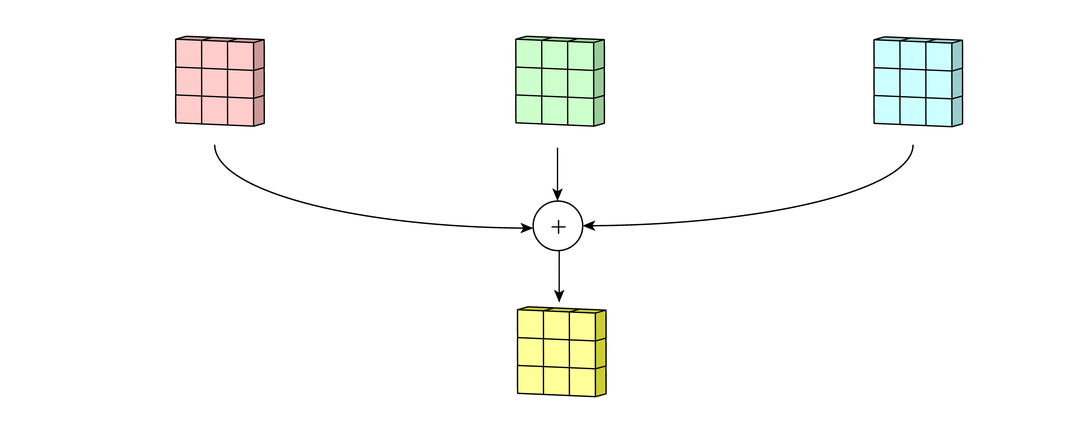
После этого к каждому значению матрицы добавляется одинаковое число – значение смещения данного фильтра. Полученная матрица составляет один канал выходной карты признаков.

После того, как будут получены каналы для каждого из фильтров, матрицы объединяются в единый тензор, благодаря чему на выходе снова получается изображение, с другим числом каналов и, возможно, другим размером.

Параметры свёрточного слоя

• Число признаков (filters count, fc) – это количество фильтров, которые есть в слое.
• Размер фильтров (filter size, fs) – это высота и ширина тензора фильтров. Обычно является нечётным числом, наиболее часто используются фильтры размером 3 или 5.
• Шаг свёртки (stride, S) – это количество пикселей, на которое перемещается матрица фильтра по входному изображению. Когда шаг равен 1, фильтры перемещаются по одному пикселю за раз. Когда шаг равен 2, тогда фильтры перескакивают на 2 пикселя за раз. Чем больше шаг, тем меньшего размера карты признаков получаются на выходе.
• Дополнения нулями (padding, P) – количество пикселей, которые добавляются с каждого края изображения. Это позволяет избежать уменьшения изображения на размер фильтра, поскольку фильтр может накладываться лишь в тех местах, в которых под каждым значением фильтра будет значение входного изображения.

Таким образом, входными параметрами свёрточного слоя являются:

• тензор размером W₁xH₁xD₁;
• 4 гиперпараметра: fc, fs, S, P;

А выходным параметром слоя является тензор размером W₂xH₂xD₂, где W₂ = (W₁ — fs + 2P) / S + 1, H₂ = (H₁ – fs + 2P) / S + 1, D₂ = fc.

Подробнее про арифметику свёрточного слоя и применение параметров padding и stride можно почитать здесь: convolution arithmetic tutorial.

Обучаемые параметры в сверточном слое

В свёрточном слое обучаются только фильтры и веса смещения, а потому общее число обучаемых параметров равно fc·(fs·fs·fd+1), то есть число элементов каждого фильтра плюс один параметр смещения умножается на количество самих фильтров. Благодаря тому, что фильтр, который проходится по изображению, не изменяется во время самого прохождения, получается, что число обучаемых параметров во много раз меньше, чем у полносвязной сети.

Примеры некоторых фильтров

Для обработки изображений (не только нейросетями) нередко требуется выделять границы, повышать резкость или применять размытие. Для подобных целей были получены фильтры, которые сегодня зачастую встраиваются в различные графические редакторы, в которых имеется возможность применять свёрточные преобразования. Ниже вы можете посмотреть на работу некоторых из таких фильтров:

Без измененийВыделение границ по XВыделение границ по YВыделение границПовышение резкостиРазмытиеРазмытие Гаусса