Причина ограничения количества ядер в процессорах

Введение

С точки зрения параллелизма, как пути для увеличения эффективности вычислительных процедур, изучаются следующие случаи:

Случай, когда параллельные вычисления не представляются возможными или обладают малой эффективностью. Как правило, это связано с тем, что любой шаг исполняемого алгоритма зависит от результата или статуса выполнения предыдущего шага.
Случай Embarrassingly parallel, что означает случай чрезвычайной параллельности. Это абсолютно иной тип задач, для которых нет необходимости в приложении больших усилий для подразделения их на несколько отдельных параллельных подзадач.

Для второго типа, как правило, не существует прямой зависимости между этими параллельными задачами, то есть результаты их решения не могут влиять друг на друга. Распараллеливание может повлечь дополнительные расходы, а именно:

На синхронизацию.
На смену контекста и прочее.

Когда задача плохо разбивается на параллельные вычисления, то такие дополнительные расходы способны привести к уменьшению производительности. С другой стороны, когда задача легко может быть поделена на набор параллельных задач, то она может быть подвергнута масштабированию не только по ядрам одной машины, но и в горизонтальном направлении, то есть, на множество разных машин. Как следствие могут появиться проблемы, связанные с сохранением и объединением результатов.

Конкретные многоядерные компьютеры с 1 млн и более ядер ЦП

Некоторые компьютеры, построенные на основе многоядерных процессоров, имеют один миллион или более отдельных ядер ЦП. Примеры включают:

Sunway TaihuLight, массово-параллельный (10M CPU ядер) китайский суперкомпьютер, когда-то один из самых быстрых суперкомпьютеров в мире, использующий нестандартную многоядерную архитектуру[нужна цитата ]. По состоянию на ноябрь 2018 года, третий по скорости суперкомпьютер в мире (согласно рейтингу TOP500 list), китайский Sunway TaihuLight, получает свою производительность от 40 960 SW26010 многоядерные процессоры, каждый из которых содержит 256 ядер.
Gyoukou (Японский: 暁光 Хепберн: гёкё, рассветный свет), а суперкомпьютер разработан ExaScaler и PEZY Computing.
Спинакер, массивно-параллельный (1M CPU ядер) многоядерный процессор, построенный как часть Проект человеческого мозга

Демонстрация

Задачу, выполняемую системой с улучшенными ресурсами по сравнению с аналогичной исходной системой, можно разделить на две части:

часть, не извлекающая выгоду из улучшения системных ресурсов;
часть, извлекающая выгоду из улучшенных системных ресурсов.

Пример. — Компьютерная программа, обрабатывающая файлы на диске. Часть программы начинается с чтения каталога на диске и создания списка файлов в памяти. Затем другая часть программы передает каждый файл в поток для обработки. Часть, которая читает каталог и создает список файлов, не может быть ускорена на параллельном компьютере, но часть, которая обрабатывает файлы, может.

Время выполнения всей задачи перед улучшающим ресурсом отмечен T . Он включает время выполнения части, не получающей выгоды от улучшения ресурсов, и время выполнения той части, которая получает от этого выгоду. Процент времени выполнения всей задачи относительно части, извлекающей выгоду из улучшения ресурсов, до улучшения ресурсов отмечен стр . То, что касается части, не получающей от этого выгоды, поэтому 1 — p . Он приходит

Тзнак равно(1-п)Т+пТ.{\ Displaystyle T = (1-p) T + pT.}

Это выполнение части, извлекающей выгоду из улучшения ресурсов, которая ускоряется в s раз после улучшения ресурсов. Следовательно, время выполнения части, не получающей выгоды, остается прежним, в то время как время выполнения части, извлекающей выгоду из этого, становится прежним.

пsТ.{\ displaystyle {\ frac {p} {s}} T.}

Таким образом, теоретическое время выполнения T ( с ) всей задачи после улучшения ресурсов составляет

Т(s)знак равно(1-п)Т+пsТ.{\ Displaystyle T (s) = (1-p) T + {\ frac {p} {s}} T.}

Закон Амдала выражает теоретическое ускорение задержки выполнения всей задачи при постоянной нагрузке выполнения C, что дает

Sзадержка(s)знак равноТПРОТИВТ(s)ПРОТИВзнак равноТТ(s)знак равно11-п+пs.{\ displaystyle S _ {\ text {latency}} (s) = {\ frac {TC} {T (s) C}} = {\ frac {T} {T (s)}} = {\ frac {1 } {1-p + {\ frac {p} {s}}}}.}

Принципы

Принцип Дилберта

В компаниях существует тенденция к повышению некомпетентных сотрудников до менеджеров с целью устранить их от рабочего процесса.

Принцип Парето (правило 80/20)

По большей части в жизни всё распределяется неравномерно.

80% программы можно написать за 20% времени (и на самые сложные 20% уходят остальные 80% времени).
20% усилий дают 80% результата.
20% работы создают 80% прибыли.
20% ошибок приводят к 80% падений программы.
20% функций используется 80% времени.

Принцип единственной ответственности

Каждый объект должен иметь одну ответственность и эта ответственность должна быть полностью инкапсулирована в класс.

YAGNI

Всегда реализуйте функции только тогда, когда они вам реально нужны, а не тогда, когда вам кажется, что они вам понадобятся в будущем.

Заблуждения распределённых вычислений

Сеть надёжна.
Задержка нулевая.
Пропускная способность бесконечна.
Сеть безопасна.
Топология не меняется.
Администратор только один.
Стоимость пересылки нулевая.
Сеть однородна.

Контраст с многоядерной архитектурой

Многоядерные процессоры отличаются от многоядерные процессоры быть оптимизированным с самого начала для более высокой степени явный параллелизм, а также для более высокой пропускной способности (или меньшего энергопотребления) за счет задержки и меньшего однопоточная производительность.

Более широкая категория многоядерные процессоры, напротив, обычно предназначены для эффективного запуска обе параллельно и серийный код, и поэтому уделяйте больше внимания высокому однопоточная производительность (например, выделить больше кремния на вышедшее из строя исполнение, Глубже трубопроводы, более суперскалярный исполнительные единицы и более крупные кеши общего назначения) и Общая память. Эти методы выделяют ресурсы среды выполнения для выявления неявного параллелизма в одном потоке. Они используются в системах, где они непрерывно эволюционировали (с обратной совместимостью) от одноядерных процессоров. Обычно они имеют «несколько» ядер (например, 2,4,8) и могут быть дополнены множеством ядер. ускоритель (например, GPU ) в гетерогенная система.

Ускорение и эффективность

Ускорение (speedup), получаемое при использовании параллельного алгоритма для p процессоров, по сравнению с последовательным вариантом выполнения вычислений определяется величиной:

Sp(n)=T1(n)/Tp(n)

т.е. как отношение времени решения задач на скалярном процессоре(Оценка T1 определяет время выполнения алгоритма при использовании одного процессора и представляет, тем самым, время выполнения последовательного варианта алгоритма решения задачи) к времени выполнения параллельного алгоритма (величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи).

Эффективность (efficiency) использования параллельным алгоритмом процессоров при решении задачи определяется соотношением:

Ep(n)=T1(n)/(pTp(n))=Sp(n)/p

Величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры реально задействованы для решения задачи.

Закон Амдала

Иллюстрирует ограничение роста производительности вычислительной системы с увеличением количества вычислителей.

Джин Амдал сформулировал закон в 1967 году, обнаружив простое по существу, но непреодолимое по содержанию ограничение на рост производительности при распараллеливании вычислений:

Согласно этому закону, ускорение выполнения программы за счёт распараллеливания её инструкций на множестве вычислителей ограничено временем, необходимым для выполнения её последовательных инструкций.

Пусть необходимо решить некоторую вычислительную задачу. Предположим, что её алгоритм таков, что доля a от общего объёма вычислений может быть получена только последовательными расчётами, а, соответственно, доля 1 — a может быть распараллелена идеально (то есть время вычисления будет обратно пропорционально числу задействованных узлов p). Тогда ускорение, которое может быть получено на вычислительной системе из p процессоров, по сравнению с однопроцессорным решением не будет превышать величины:

Таблица показывает, во сколько раз быстрее выполнится программа с долей последовательных вычислений a при использовании p процессоров.

╔═════════╦════════════════╦═════════════╦══════════╗║   a/p   ║       10       ║     100     ║ 1000     ║╠═════════╬════════════════╬═════════════╬══════════╣║        ║   10           ║   100       ║ 1000     ║ ║ 10%     ║   5.263        ║   9.174     ║ 9.910    ║║ 25%     ║   3.077        ║   3.883     ║ 3.988    ║║ 40%     ║   2.174        ║   2.463     ║ 2.496    ║╚═════════╩════════════════╩═════════════╩══════════╝

Из таблицы видно, что только алгоритм, вовсе не содержащий последовательных вычислений (a = 0), позволяет получить линейный прирост производительности с ростом количества вычислителей в системе. Если доля последовательных вычислений в алгоритме равна 25%, то увеличение числа процессоров до 10 дает ускорение в 3,077 раза, а увеличение числа процессоров до 1000 даст ускорение в 3,988 раза.

Отсюда же очевидно, что при доле последовательных вычислений a общий прирост производительности не может превысить 1/a. Так, если половина кода — последовательная, то общий прирост никогда не превысит двух.

Закон Амдала показывает, что прирост эффективности вычислений зависит от алгоритма задачи и ограничен сверху для любой задачи с a<>0. Не для всякой задачи имеет смысл наращивание числа процессоров в вычислительной системе.

Более того, если учесть время, необходимое для передачи данных между узлами вычислительной системы, то зависимость времени вычислений от числа узлов будет иметь максимум. Это накладывает ограничение на масштабируемость вычислительной системы, то есть означает, что с определенного момента добавление новых узлов в систему будет увеличивать время расчёта задачи.

Густафсон Закон

Закон Густафсона также пытался объяснить отношения между количеством процессоров, коэффициентов сериализации и соотношениями ускорения, как показано на рисунке 1.12, но угол закона Густафсона и закона о амдрах. Аналогично, соотношение ускорения определяется как энергопотребление в системе до оптимизации, разделенного оптимизированной системой.

Согласно закону Густафсона, мы можем легко обнаружить, что если коэффициент сериализации небольшой, сравнительное соотношение велико, то отношение ускорения составляет количество процессоров. Пока вы продолжаете накапливаться процессоры, вы можете получить более быструю скорость.

Закон и закону Амдаля и закона Густафсона разные. Нельзя сказать, что есть ошибка, но оба из разных углов, чтобы увидеть результаты проблемы, их бокового фокуса отличается.

Amdahl подчеркивает: Когда соотношение серийной замены, соотношение ускорения — это верхний предел, независимо от участия ЦП в вашем стеке, вы не можете пробиться через этот предел.

Законные отношения Густафсона: Если доля кода, который может быть достаточно оплаты, достаточно, соотношение ускорения может расти с количеством процессоров.

В целом улучшить методы производительности: я хочу для меняУвеличьте систему параллельноПропорция, увеличить количество процессоров.

Законы

Закон Голла

Работающая сложная система обязательно произошла от работавшей простой системы. Сложная система, разработанная с нуля, никогда не работает, и её невозможно исправить так, чтобы она заработала. Нужно начать заново, с простой работающей системы.

Закон Гудхарта

Любая наблюдаемая статистическая закономерность склонна разрушаться, как только на неё оказывается давление с целью управления ею.
Когда мерило становится целью, оно перестаёт быть хорошим мерилом.
Мэрилин Стратерн

Тесты без утверждений удовлетворяют ожиданиям по покрытию кода, несмотря на то, что такая метрика создавалась для того, чтобы программа была хорошо проверена.
Оценка эффективности разработчика на основе количества строк, внесённых в проект, приводит к неоправданному раздуванию кода.

Цикл шумихи и закон Амара

Мы склонны переоценивать влияние технологии в краткосрочной перспективе и недооценивать его в долгосрочной.
После появления технологии её популярность доходит до пика раздутых ожиданий, затем ныряет во впадину разочарования, поднимается по склону просветления и выходит на плато продуктивности

Закон Хирама

При достижении достаточного количества пользователей API уже неважно, какие его особенности вы обещали всем: для любой из возможных особенностей поведения вашей системы найдётся зависящий от неё пользователь.

Закон Кернигана

Отладка кода в два раза тяжелее, чем его написание. Поэтому, если вы пишете код на пределе умственных возможностей, вам, по определению, не хватит ума, чтобы его отлаживать.

Закон Мёрфи

Всё, что может пойти не так, пойдёт не так.
Если что-то может пойти не так, это случится, причём в наихудший из возможных моментов.

Закон Патта

В технологическом секторе доминируют два типа людей: те, кто разбирается в том, что они не контролируют, и те, кто контролирует то, в чём они не разбираются.
В любой технической иерархии со временем вырабатывается инверсия компетентности.

Приложения

Применение в исследованиях

Закон Амдала предполагает, что вычислительные требования останутся неизменными при увеличении вычислительной мощности. Другими словами, анализ одних и тех же данных займет меньше времени при большей вычислительной мощности.

Густафсон, с другой стороны, утверждает, что большая вычислительная мощность приведет к более тщательному и полному анализу данных: пиксель за пикселем или единица за единицей, а не в большем масштабе. Там, где было бы невозможно или практически невозможно смоделировать воздействие ядерного взрыва на каждое здание, автомобиль и их содержимое (включая мебель, прочность конструкции и т. Д.), Потому что такой расчет потребовал бы больше времени, чем было доступно для обеспечения Ответ: увеличение вычислительной мощности побудит исследователей добавлять больше данных для более полного моделирования большего числа переменных, что дает более точный результат.

Применение в повседневных компьютерных системах

Закон Амдала обнаруживает ограничение, например, в способности нескольких ядер сокращать время, необходимое компьютеру для загрузки операционной системы и готовности к работе. Если предположить, что процесс загрузки был в основном параллельным, учетверенное увеличение вычислительной мощности в системе, для которой загружалась одна минута, могло бы сократить время загрузки до чуть более пятнадцати секунд. Но все большее и большее распараллеливание в конечном итоге не могло бы ускорить загрузку, если бы какая-либо часть процесса загрузки была изначально последовательной.

Закон Густафсона утверждает, что четырехкратное увеличение вычислительной мощности вместо этого приведет к аналогичному увеличению ожиданий относительно того, на что будет способна система. Если время загрузки в одну минуту приемлемо для большинства пользователей, то это отправная точка для расширения возможностей и функций системы. Время, необходимое для загрузки операционной системы, будет таким же, то есть одна минута, но новая система будет включать больше графических или удобных для пользователя функций.

Ограничения

Некоторые проблемы не имеют существенно больших наборов данных. Например, обработка одной точки данных на каждого гражданина мира увеличивается всего на несколько процентов в год. Принципиальный момент закона Густафсона состоит в том, что такие задачи вряд ли могут быть наиболее плодотворными приложениями параллелизма.

Алгоритмы с нелинейным временем выполнения могут столкнуться с трудностями при использовании преимуществ параллелизма, «раскрытого» законом Густафсона. Снайдер указывает на O (N3) означает, что удвоение параллелизма дает лишь примерно 26% увеличение размера проблемы. Таким образом, несмотря на то, что можно использовать обширный параллелизм, это может принести мало преимуществ по сравнению с исходным, менее параллельным решением, однако на практике все еще были значительные улучшения.

Хилл и Марти подчеркнем также, что методы ускорения последовательного выполнения по-прежнему необходимы даже для многоядерных машин. Они указывают, что неэффективные в локальном масштабе методы могут быть эффективными в глобальном масштабе, если они сокращают последовательную фазу. Кроме того, Ву и Ли изучили влияние энергии и мощности на будущие многоядерные процессоры на основе закона Амдала, показав, что асимметричный многоядерный процессор может достичь наилучшей возможной энергоэффективности за счет активации оптимального количества ядер, учитывая, что степень параллелизма известна до выполнения .

Что такое закон Амдаля и для чего он нужен?

Определение этого закона устанавливает, что: «Улучшение производительности системы за счет чередования одного из ее компонентов ограничивается долей времени, в течение которого компонент используется».

Выше вы можете увидеть формулу, где:

Fm — временной интервал, в котором система использует расширенную подсистему.
Am — это коэффициент улучшения, введенный в систему.
Ta — это старая среда выполнения.
Tm — это улучшенная среда выполнения.

Эту формулу можно переписать, используя определение увеличения скорости для расчета прироста скорости (A):

С определением этого закона, вероятно, вы остались прежними, поэтому мы собираемся объяснить вам это своими словами; Этот закон говорит нам о том, что улучшение производительности системы (понимание набора частей, таких как ПК), когда вы меняете одну часть, ограничивается временем использования этого компонента.

Другими словами, на примере: повышение производительности вашего ПК при изменении Оперативная память память ограничена временем, в течение которого вы собираетесь использовать указанный компонент. Теперь лучше, правда? Но это наверняка поднимет другой вопрос: какое время, которое вы используете компонент, будет связано с улучшением производительности? Чтобы понять это, давайте посмотрим на другой пример.

Если в программе для ПК скорость выполнения алгоритма (такого как работа процессора) составляет 30% времени выполнения от общего времени, которое требуется программе для выполнения команды, и нам удается запустить этот алгоритм в половине случаев у нас будет:

Ам = 2
Fm = 0.3
A = 1.8

Это означает, что скорость выполнения программы улучшится в 1.8 раза, и то только за счет изменения одной из ее подсистем.

Определение

Густафсон оценил ускорение S получено с помощью N процессоров (вместо одного) для задачи с порядковой дробью s (который не выигрывает от параллелизма) следующим образом:

S=N+(1−N)s{ Displaystyle S = N + (1-N) s}

Используя различные переменные, закон Густафсона можно сформулировать следующим образом:[нужна цитата ]

Sзадержка(s)=1−п+sп,{ displaystyle S _ { text {latency}} (s) = 1-p + sp,}

куда

S_{задержка} — теоретическое ускорение задержки выполнения всей задачи;
s — это ускорение задержки выполнения той части задачи, которая выигрывает от улучшения ресурсов системы;
п это процент исполнения нагрузка всей задачи, касающейся той части, которая извлекает выгоду из улучшения ресурсов системы до улучшения.

Закон Густафсона устраняет недостатки Закон Амдала, который основан на предположении фиксированной размер проблемы, то есть рабочей нагрузки выполнения, которая не изменяется по мере улучшения ресурсов. Вместо этого закон Густафсона предполагает, что программисты склонны устанавливать размер задач так, чтобы полностью использовать вычислительную мощность, которая становится доступной по мере увеличения ресурсов. Следовательно, если доступно более быстрое оборудование, более крупные проблемы могут быть решены за то же время.

Влияние закона Густафсона заключалось в изменении[нужна цитата ] цель исследования — выбрать или переформулировать проблемы так, чтобы было возможно решение более крупной проблемы за то же время. В некотором смысле закон переопределяет эффективность из-за возможности того, что ограничения, налагаемые последовательной частью программы, могут быть устранены путем увеличения общего объема вычислений.

Закон Густавсона-Барсиса

Оценка максимально достижимого ускорения выполнения параллельной программы, в зависимости от количества одновременно выполняемых потоков вычислений («процессоров») и доли последовательных расчётов.

Закон Густафсона — Барсиса выражается формулой:

s — доля последовательных расчётов в программе,

n — количество процессоров

Данную оценку ускорения называют ускорением масштабирования (scaled speedup), так как данная характеристика показывает, насколько эффективно могут быть организованы параллельные вычисления при увеличении сложности решаемых задач.

При оценке ускорения параллельного выполнения закон Амдала предполагает, что объем задачи остается постоянным. Величина ускорения по закону Амдала показывает, во сколько раз меньше времени потребуется параллельной программе для выполнения.

Однако величину ускорения можно рассматривать и как увеличение объема выполненной задачи за постоянный промежуток времени. Закон Густафсона появился именно из этого предположения.

Ускорение масштабирования определяется как отношение объема вычислений, выполненных с использованием многопоточности, к объему вычислений, выполненных последовательно за один и тот же промежуток времени.

Отношение к закону убывающей отдачи

Закон Амдала часто смешивают с закон убывающей доходности, тогда как только частный случай применения закона Амдала демонстрирует закон убывающей отдачи. Если выбрать оптимально (с точки зрения достигнутого ускорения), что нужно улучшить, то по мере улучшения можно будет увидеть монотонно убывающие улучшения. Если, однако, выбрать неоптимальный компонент после улучшения субоптимального компонента и перехода к улучшению более оптимального компонента, можно увидеть увеличение прибыли

Обратите внимание, что часто рационально улучшать систему в «неоптимальном» в этом смысле порядке, учитывая, что некоторые улучшения сложнее или требуют большего времени на разработку, чем другие

Закон Амдала действительно представляет закон убывающей отдачи, если при рассмотрении того, какого рода отдачу можно получить, добавляя больше процессоров к машине, если выполняется вычисление фиксированного размера, которое будет использовать все доступные процессоры в полную силу. Каждый новый процессор, добавленный в систему, будет добавлять меньше полезной мощности, чем предыдущий. Каждый раз, когда количество процессоров удваивается, коэффициент ускорения будет уменьшаться, поскольку общая пропускная способность приближается к пределу 1 / (1 —п).

Этот анализ не учитывает другие потенциальные узкие места, такие как пропускная способность памяти и пропускная способность ввода / вывода. Если эти ресурсы не масштабируются вместе с количеством процессоров, то простое добавление процессоров дает еще меньшую отдачу.

Следствием закона Амдала является то, что для ускорения реальных приложений, которые имеют как последовательные, так и параллельные части, гетерогенные вычисления техники требуются. Например, гетерогенный процессор CPU-GPU может обеспечивать более высокую производительность и энергоэффективность, чем процессор только CPU или GPU.

Иногда разочаровывающая работа

Некоторые приложения, такие как обработка изображений, очень хорошо используют параллелизм. В их случае p может быть близко к 95%.
Другие, такие как численный анализ будет в состоянии извлечь выгоду из изменения алгоритма (например, замена метода Гаусса-Зейделя с помощью метода Якоби, который сходится медленнее, но является полностью параллелизуемое).

Остальные случаи неутешительны: при p = 50% переход на двухпроцессорную экономию времени составляет 25%. Переход на 12 процессоров увеличивает экономию времени до 46%.

Примечание. — Закон Амдала здесь рассматривается в случае системы, в которой все процессоры предназначены для одного пользователя и для потоков одного и того же процесса. Этот случай встречается не всегда. На практике результаты будут еще хуже, если мы не будем управлять сходством процессоров, которое гарантирует, что одни и те же процессоры возобновляют в максимально возможной степени одни и те же процессы, чтобы избежать несвоевременной перезагрузки кеша .

Увеличение p

Случай, когда p явно находится близко к 100%, — это когда процессоры выполняют разные программы: будучи независимыми, они ipso facto распараллеливаются, и, более того, без малейших усилий, которые необходимо предпринять для обеспечения этого распараллеливания. На этом этапе остаются проблемы, которые:

время, прошедшее для данного приложения, напрямую не сокращается: четырехчасовая симуляция будет продолжать ждать результатов четыре часа (но будет меньше замедляться другими процессами, если будет заявлено, что процессор выделен для нее);
кэш — память и кэш диска становится все более переполнены данными, принадлежащих к различным процессам, и они должны быть, как ожидается, увеличиваются в размерах, соответственно. Проблема исчезает для кэш-памяти, когда она находится на самом микропроцессоре, который, в свою очередь, регулирует эффекты масштабирования.

Мотивация

Согласованность кеша это проблема, ограничивающая масштабирование многоядерных процессоров. Процессоры Manycore могут обойти это с помощью таких методов, как передача сообщений,блокнотная память, DMA,разделенное глобальное адресное пространство, или кеши только для чтения / некогерентные. Многоядерный процессор, использующий сеть на чипе и локальная память дает программному обеспечению возможность явно оптимизировать пространственную компоновку задач (например, как видно в инструментах, разработанных для TrueNorth ).

Многоядерные процессоры могут иметь больше общего (концептуально) с технологиями, возникшими в высокопроизводительные вычисления Такие как кластеры и векторные процессоры.

Графические процессоры можно рассматривать как форму многоядерных процессоров, имеющих несколько блоки обработки шейдеров и подходит только для высокопараллельного кода (высокая пропускная способность, но чрезвычайно низкая производительность одного потока).

Закон Амдала, сверх масштабируемые и сверх линейные по скорости исполнения алгоритмы

Закон Амдала определяет метод, при помощи которого возможно смоделировать потенциальный выигрыш в производительности при организации параллельных вычислений. Ускорение (speedup), которое получается при использовании параллельного алгоритма для p процессоров, в сравнении с последовательным вариантом реализации вычислений определяется следующей формулой:

Sp(n) = T1(n) / Tp(n)

То есть, это отношение времени решения задач на скалярном процессоре (оценка T1 задаёт время исполнения алгоритма при работе на одном процессоре, то есть определяет время исполнения последовательной версии алгоритма решения задачи) к времени исполнения параллельного алгоритма (значение n используется для параметризации уровня вычислительной сложности решаемой задачи и может представлять, к примеру, количество входных данных задачи).

Эффективность (efficiency) применения параллельным алгоритмом процессоров для решения задачи может быть определена по следующему соотношению:

Ep(n) = T1(n) / (pTp(n)) = Sp(n) / p

Значение эффективности может определить среднюю долю времени исполнения алгоритма, в течение которой процессоры фактически используются для решения задачи. Закон Амдала, по сути, выполняет иллюстрацию ограничения роста производительности вычислительной системы с ростом числа вычислительных модулей.

Джин Амдал вывел формулировку своего закона в 1967-ом году, выявив очень простое по своей сути, но непреодолимое по содержанию ограничение роста производительности при осуществлении распараллеливания вычислительных операций, в следующем виде:

В соответствии с этим законом, ускорение исполнения программы за счёт распараллеливания её операций на множестве вычислительных модулей ограничено временем, которое требуется для исполнения её последовательных инструкций.

Допустим, что требуется выполнить решение некоторой вычислительной задачи. Можно предположить, что её алгоритм таков, что долю «a» от общего объёма вычислительных операций можно получить только при помощи последовательных расчётов, а, соответственно, долю «1 — a» можно распараллелить идеально. То есть время вычислительных процедур является обратно пропорциональным количеству используемых узлов «p».

В этом случае ускорение, которое можно получить на вычислительной системе из p процессорных модулей, по сравнению с однопроцессорным вариантом решения не будет больше следующего значения:

Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ

Таблица, приведённая ниже, может показать, во сколько раз быстрее исполнится программа с долей последовательных вычислений «a», если задействовать «p» процессорных модулей:

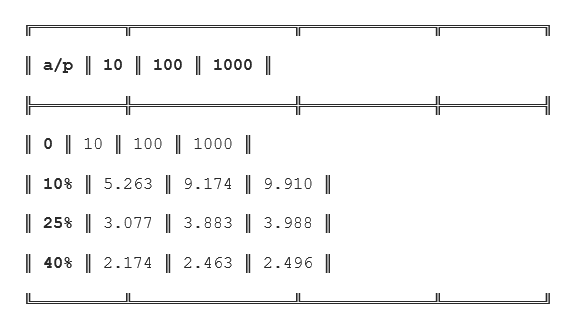Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ

Из данной таблицы следует, что только алгоритм, который совсем не содержит последовательных вычислений (a = 0), даёт возможность получения линейного прироста производительности при росте количества вычислительных модулей в системе. Если доля последовательных вычислений в алгоритме равняется двадцати пяти процентам, то увеличение количества процессорных модулей до десяти позволяет получить ускорение только в 3,077 раза, а увеличение числа процессорных модулей до тысячи даст ускорение всего лишь в 3,988 раза.

Отсюда же следует, что при доле последовательных вычислений «a» суммарный прирост производительности не может превысить значения «1/a». Так, если половина операций являются последовательными, то общий прирост никогда не превысит двух. Закон Амдала утверждает, что прирост эффективности вычислительных процедур имеет зависимость от алгоритма задачи и ограничен сверху для любой задачи с «a меньше или больше 0». Не для каждой задачи имеет смысл наращивать количество процессорных модулей в вычислительной системе

Более того, если принять во внимание время, которое необходимо для передачи данных между модулями вычислительной системы, то зависимость времени вычислений от количества узлов будет максимальной