8.1. Дискретизация аналоговых сигналов. Спектр дискретного сигнала
В настоящее время в связи с широким распространением цифровых систем передачи и обработки информации возникла необходимость изучения принципов формирования и методов оценки характеристик таких сигналов. Как известно из предыдущего материала, формирование цифрового сигнала включает в себя следующие операции: дискретизацию аналогового сигнала во времени, квантование дискретного сигнала по уровню и перекодирование значений квантованного сигнала из одной системы счисления в другую (в подавляющем большинстве случаев – в двоичную). Мы начнем с рассмотрения спектральных характеристик дискретного сигнала.
Напомним, что дискретный сигнал (или дискретная последовательность) формируется при помощи перемножителя (рис. 8.1), на один из входов которого поступает аналоговый сигнал , а на второй – последовательность коротких импульсов с периодом следования , значение которого определяется теоремой Котельникова
,
где или – верхняя граничная частота аналогового сигнала .
Тогда дискретный сигнал может быть описан выражением
. (8.1)
Вычислим спектр дискретного сигнала. В первую очередь, рассмотрим второй сомножитель выражения (8.1)
. (8.2)
Этот сомножитель представляет собой математическое описание периодической последовательности импульсов. Обычно при осуществлении операции дискретизации форма импульса выбирается прямоугольной. Поэтому в дальнейшем будем полагать, что представляет собой периодическую последовательность прямоугольных импульсов амплитудой и длительностью , следующих с периодом .
Как известно, периодическая последовательность прямоугольных импульсов может быть представлена рядом Фурье, который для рассматриваемого случая принимает вид
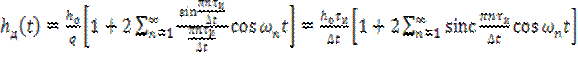. (8.3)
где , – скважность,. Тогда с учетом (8.3) выражение (8.1) принимает вид
Тогда с учетом (8.3) выражение (8.1) принимает вид
. (8.4)
Применим к (8.4) прямое преобразование Фурье
.
Подстановка в эту формулу выражения (8.4) дает
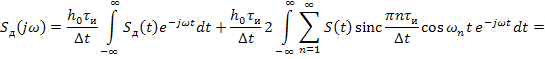
. (8.5)
Интеграл первого слагаемого в (8.5) представляет собой спектр исходного аналогового сигнала. Представим второе слагаемое в (8.5) в виде
. (8.6)
Учитывая, что , запишем
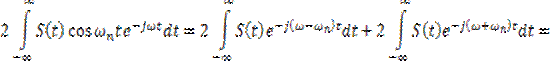
. (8.7)
Тогда с учетом (8.6) и (8.7) выражение (8.5) принимает вид
. (8.8)
Здесь пределы суммирования составляют в виду того, что спектр распространяется на область отрицательных частот.
Дальнейший спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса и выражение (8.8) запишется следующим образом
. (8.9)
Если устремить , т.е. перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.
, (8.10)
то с учетом того, что , спектральная функция дискретного сигнала окончательно принимает вид
. (8.11)
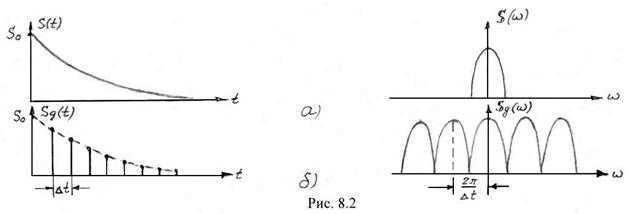
На рис. 8.2 а) представлен аналоговый сигнал и условное изображение модуля его спектральной функции , а на рис. 8.2б – дискретный сигнал и модуль его спектра . Из выражения (8.11) и рис. 8.2 следует, что спектр дискретного сигнала представляет собой бесконечную последовательность копий спектра исходного аналогового сигнала , причем эта последовательность носит периодический характер. Расстояние по оси частот между отдельными копиями составляет (или ), что соответствует периоду последовательности копий на оси частот. Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации.
8.8. Методы синтеза цифровых фильтров
Под синтезом цифрового фильтра понимают определение его масштабных коэффициентов и , при которых обеспечиваются требуемые его характеристики.
Все методы синтеза цифровых фильтров можно разделить на две группы:
- методы, использующие в качестве прототипов, соответствующие аналоговые фильтры;
- прямые методы, использующие непосредственный поиск масштабных коэффициентов, обеспечивающих оптимальные значения характеристик фильтров. Поскольку методы синтеза аналоговых фильтров хорошо разработаны, методы первой группы нашли наиболее широкое распространение. Кратко остановимся на этих методах.
Синтез цифрового фильтра на основе перехода от дифференциального уравнения аналогового фильтра к разностному уравнению цифрового фильтра. Этот метод был использован выше при определении структуры цифрового фильтра, аналогичного – цепи (выражение (8.31) и рис. 8.2).
Синтез цифрового фильтра на основе дискретизации импульсной характеристики аналогового фильтра прототипа. Суть метода состоит в том, что импульсная характеристика фильтра – прототипа подвергается дискретизации с интервалом , т.е. определяется . Далее с помощью -преобразование определяется системная функция
, (8.53)
которая и дает структуру фильтра.
Синтез цифрового фильтра на основе перехода передаточной функции аналогового фильтра к системной функции цифрового фильтра. Переход от к в этом случае осуществляется с помощью так называемого билинейного преобразования
, (8.54)
т.е. в заменяют в соответствии с выражением (8.54). Оценка качества каждого метода приведена в рекомендованной литературе.
Список рекомендуемой литературы
1. С.И. Баскаков. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000
2. И.С. Гоноровский, М.П. Демин. Радиотехнические цепи и сигналы – М.: Радио и связь, 1994
3. Радиотехнические цепи и сигналы. Учебные пособия для ВУЗов/ под ред. К.А. Самойло – М.: Радио и связь, 1982
4. С.И. Баскаков. Радиотехнические цепи и сигналы. Руководство по решению задач. – М.: Высшая школа, 2002
5. Радиотехнические цепи и сигналы. Примеры и задачи/ под ред. И.С. Гоноровского. – М.: Радио и связь, 1989
6. Радиотехнические цепи и сигналы. Задачи и задания/ под ред. А.Н. Яковлева. – М.: Инфа-М, изд-во НГТУ, 2003г.
7. М.Т. Иванов, А.Б. Сергиенко, В.И. Ушаков. Теоретические основы радиотехники. – М.: Высшая школа, 2002г.
DVB-C
Этот стандарт изначально создан для передачи по кабелю (C — Cable) — среде намного стабильнее воздуха, поэтому позволяет использовать более высокую степень модуляции чем DVB-T, а значит и передавать больший объём информации, не используя при этом сложное кодирование. Тут мы видим созвездие 256QAM. Квадратов стало больше, размер их стал меньше. Вероятность ошибки увеличилась, а значит для передачи такого сигнала нужна более надёжная среда (или более сложное кодирование, как в DVB-T2). Такой сигнал может «рассыпаться» там, где работают аналог и DVB-T/T2, однако он так же имеет запас помехозащищённости и алгоритмы исправления ошибок.
В силу большей вероятности ошибки, параметр MER для 256-QAM нормирован уже в 32дБ.
Счётчик ошибочных бит поднялся ещё на порядок и вычисляет уже один ошибочный бит на миллиард, но даже если их будет сотни миллионов (PRE-BER ~E-07-8), то используемый в этом стандарте декодер Рида-Соломона устранит все ошибки.
DVB-T2
Принятый в России стандарт цифрового эфирного вещания так же может быть передан по кабелю. Форма созвездия при первом взгляде может несколько удивить: Такой поворот дополнительно повышает помехозащищённость, так как приёмник знает, что созвездие должно быть повёрнуто на заданный угол, значит можно фильтровать то, что приходит без заложенного сдвига. Тут видно, что для этого стандарта нормы битовых ошибок на порядок выше и ошибки в сигнале до обработки уже не выходят за предел измерений, а составляют вполне реальные 8,6 на миллион. Для их исправления используется декодер LDPC
, поэтому параметр называется LBER. Благодаря повышенной помехозащищённости, этот стандарт поддерживает уровень модуляции 256QAM, но в данный момент в эфирном вещании используется только 64QAM.
Преимущества MER
MER (Modulation Error Ratio) — это ошибка модуляции, характеризующая отклонение реального символа от местоположения символа идеального на констелляционной диаграмме1.
По сравнению с BER параметр MER предоставляет более оперативную информацию о сигнале. Как я уже упоминал, MER является подобием параметра отношения сигнал/шум, хотя и учитывает большее число факторов, искажающих исходный радиосигнал. Значение параметра так же усредняется по времени, как и все величины, связанные с измерением мощности, но его измерение производится для каждого символа и, учитывая большие символьные скорости, накопление за одну секунду дает достаточно достоверный результат.
Вторым достоинством параметра MER является возможность его измерения с нормированной точностью. Большинство современных микросхем декодеров, на основе которых производятся приборы, позволяют вычислять MER аппаратно или на основе величин амплитуд векторов I и Q.
Под аппаратным вычислением я имею в виду возможность получения среднеквадратичного значения вектора ошибки из одного из внутренних регистров демодулятора. Во всяком случае производители микросхем утверждают, что это именно оно, и измерения, в принципе, это подтверждают. А зная среднеквадратичное значение вектора ошибки, вычислить MER уже несложно.
Использование значений амплитуд векторов квадратур для этих целей часто менее пригодно, потому что от микросхемы можно получить лишь 7 или 8 двоичных разрядов амплитуды QIвекторов. В результате динамический диапазон расчетного значения MER получается весьма низок. А разрядность регистра ошибки, напротив, часто бывает 10-, а то и 16-битная.
Погрешность измерения, связанную с неидеальными параметрами тюнера и демодулятора, можно скорректировать, имея источник сигнала с калиброванным параметром сигнал/шум. Калибровка производится для входного сигнала с добавлением только белого шума, но такой метод, тем не менее, дает весьма хороший результат.
Поэтому погрешность параметра MER для многих приборов является нормированной величиной в отличие от BER. Точность измерения BER зависит от качества приемника и демодулятора прибора, и корректировать ее невозможно. В результате измерение BER разными приборами дает близкие значения при плохом и заметно различающиеся при хорошем (при больших значениях MER).
То есть более качественный прибор показывает более низкие (более близкие к реальным) значения BER. Способность измерять низкие значения BER является хорошим индикатором качества измерительного прибора.
Если это так, возникает вопрос: «А не достаточно ли измерять один только MER для оценки качества принимаемого сигнала, ведь время измерения небольшое. Параметр предоставляет комплексную и точную информацию. С этим можно согласиться, но только в одном случае, когда к исходному сигналу примешивается только белый гауссовский шум. Как показывают практика и тестовое моделирование, при выполнении этого условия MER совпадает с SNR, и поэтому в данном случае для определения значений preBER и postBER можно воспользоваться кривыми зависимости BER от отношения SNR входного сигнала.
Время измерения BER
Большинство приборов для измерения параметров сигналов с цифровой модуляцией имеют нижнюю границу диапазона измерения параметра BER 1E-8 или 1E-9, реже — 1E-10, 1E-11. Совершенно естественно, что пользователи приборов хотят иметь границу как можно ниже, а результат измерения получать как можно быстрее. Давайте посчитаем: если мы используем модуляцию QAM-256 и символьную скорость 6,9 Мбод, то битовая скорость на входе декодера РидаСоломона будет составлять 6,9*8=55,2 Мбит/с. Если вероятность появления ошибки 1E-8, то для измерения этой величины нам надо накопить 108 бит потока данных, из которых один бит будет ошибочным. А накапливать мы их будем в течение 108/55,2×106 = 1,8 с. То есть один неправильно декодированный бит будет появляться, в среднем, раз в две секунды.
Результат, измеренный за этот промежуток времени, будет, конечно, весьма неточным. Для уменьшения случайной погрешности необходимо его усреднить хотя бы за 10 периодов измерения, то есть за 18 секунд. Если мы захотим измерить BER с нижней границей 1E-9, то для этого нам потребуется в 10 раз больше времени: 180 секунд или 3 минуты, а для получения достоверного результата 1E-11 мы должны ждать пять часов! Если использовать модуляцию более низкого порядка или более низкую символьную скорость, время измерения увеличится еще больше
Возможно, вам также будет интересно
В больших антенных решетках при соотношениях диаметра к длине волны более ста широко используются оптические схемы возбуждения и отражательные апертуры для сканирующего луча. В качестве управляющего элемента в 70% существующих ФАР применяется ферритовый волноводный фазовращатель. Главным преимуществом такого рода конструкций является отсутствие распределителя мощности на линиях передачи, что упрощает проектирование и производство антенны. Надо принять
Линии задержки с фиксированным временем задержки (ФЛЗ) используются для подстройки электрических длин многоканальных трактов, коррекции формы диаграммы направленности многоэлементной антенны, синхронизации процессов, для решения других системных или измерительных задач. Управляемый фазовращатель на сосредоточенных реактивных элементах (Фвр) при узкополосном СВЧ-сигнале на радиочастотном входе с несущей частотой f0 с помощью квазистатического (ручного или электромеханического) изменения задержки на время τ позволяет изменять
В последние три десятилетия активно развивается направление функциональной электроники, основанное, с одной стороны, на применении эффекта взаимодействия между упругими объемными и поверхностными волнами в твердом теле и электромагнитным полем — с другой. Упругие поверхностные волны часто называют поверхностными акустическими волнами (ПАВ, или, по-английски, SAW).
8.6. Z-преобразование и системная функция дискретной цепи
В выражение (8.41) входят функции . Наличие трансцендентных функций затрудняет анализ дискретных сигналов и цепей. Для упрощения анализа удобно сделать замену
, где .
При такой замене указанные трансцендентные функции комплексной переменной преобразуются в соответствующие -изображения, являющиеся алгебраическими функциями переменной . Преобразование в плоскость осуществляется при помощи следующих соотношений, связывающих координаты какой-либо точки на плоскости с координатами соответствующей точки на плоскости :
,
; . (8.43)
Например, точка с координатами , со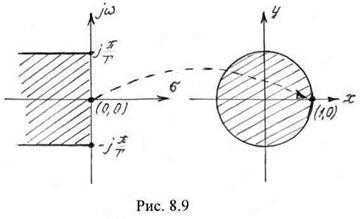
ответствует точке с координатами , (рис. 8.9). При движении точки на плоскости вдоль оси соответствующая ей точка описывает окружность единичного радиуса на -плоскости. При этом один оборот точки соответствует изменению частоты от до . Точки, лежащие в левой полуплоскости внутри области однозначно отображаются внутри круга единичного радиуса — плоскости.
Пусть дискретная последовательность представлена в виде
.
Тогда преобразование такой последовательности
,
представляет собой ряд и определено только для тех значений , при которых этот ряд сходится.
Отметим некоторые свойства — преобразования:
1. Линейность. Если последовательности соответствует — преобразование , а последовательности – z-преобразование , то
. (8.44)
2. -преобразование задержанной последовательности. Пусть последовательность является задержанной на n тактов. Ее -преобразование
. (8.45)
Таким образом, при задержке последовательности на тактов необходимо умножить ее -преобразование на .
Возвратимся к выражению (8.40). Применяя к обеим частям уравнения -преобразование с учетом второго свойства (8.45), получим:
,
откуда следует
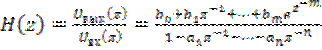. (8.46)
Отношение (8.46) называется системной функцией дискретной цепи. Системная функция для дискретной цепи играет ту же роль, что и комплексный коэффициент передачи или передаточная функция для непрерывной цепи.
Обратимся к выражению (8.39). Применяя -преобразование к обеим частям выражения, получим
,
откуда следует, что системная функция представляет собой –преобразование импульсной характеристики цепи.
Функциональные блоки процесса измерений параметров импульсных сигналов
Этапы в описанном выше процессе могут выполняться разными устройствами или одним анализатором в несколько этапов, включая измерение всех параметров импульсов. Обобщенное схематичное представление процесса показано на рис. 4.
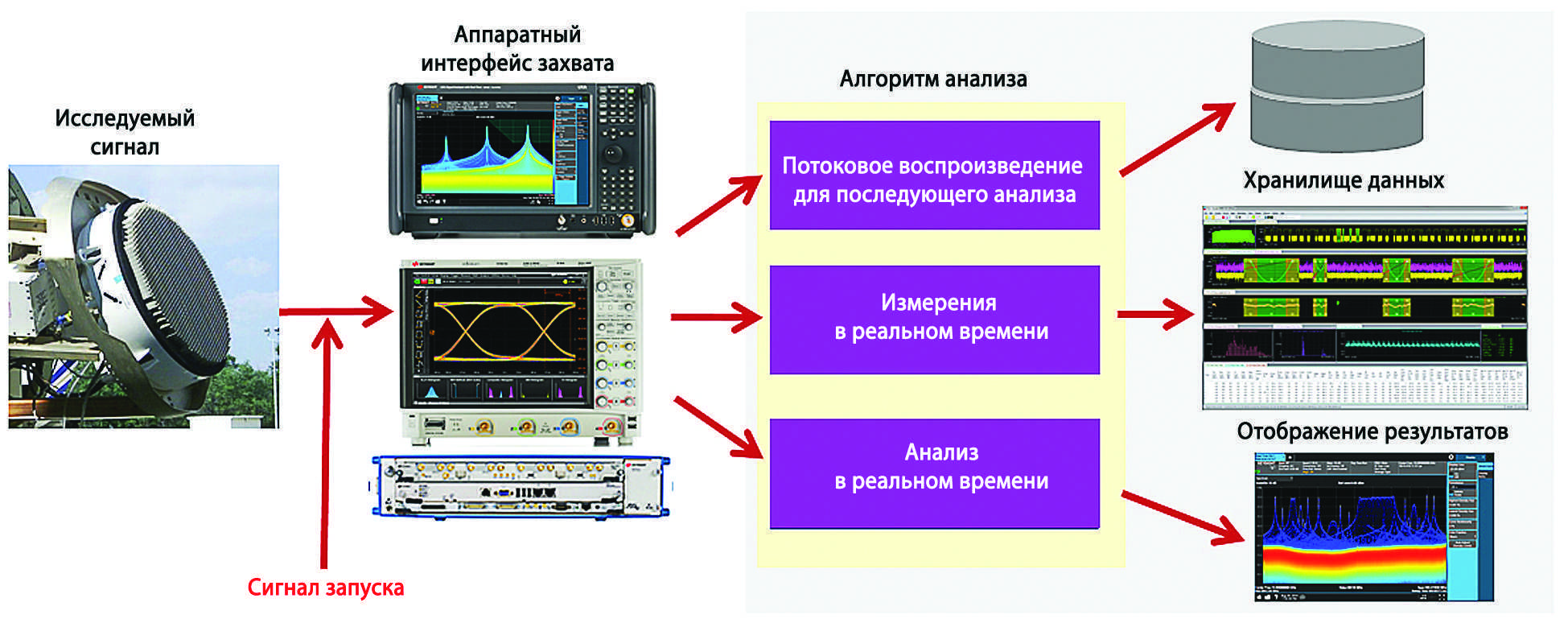
Рис. 4. Функциональные блоки процесса измерений параметров импульсов или сигнальной обстановки. Поскольку результатом захвата сигнала является набор цифровых выборок, сигнал можно записать в хранилище данных для последующей (или повторной) обработки
Аппаратные средства захвата сигнала можно реализовать по принципу оцифровки сигналов в основной полосе частот или на ПЧ и выполнить в отдельном корпусе или в виде модульных систем. Важнейшими характеристиками аппаратных средств являются полоса пропускания и динамический диапазон, хотя также важны глубина памяти, количество каналов и другие факторы, которые подробнее описаны ниже.
Алгоритмы анализа превращают оцифрованные сигналы в измерительные данные, отображаемые на экране в виде графиков и таблиц с полученными результатами. Эти алгоритмы могут быть частью общего набора инструментов векторного анализа сигналов или спектра, а также их можно интегрировать в пакеты измерительных приложений для анализа параметров импульсов. Такие приложения особенно эффективны, когда необходим более сложный анализ параметров импульсов, например статистический анализ или определение характеристик сигнальной обстановки.
Большой объем памяти имеет важное значение в случаях анализа большого количества смежных импульсных сигналов из массива данных, захваченных без пропусков, или когда доступ к исследуемому сигналу ограничен и анализ проводится позже. Хранилище захваченных данных используется при последующей обработке для получения результатов анализа и может также применяться для воспроизведения сигнала
Операции запуска могут инициировать или синхронизовать процесс измерения параметров импульсного сигнала или использоваться для привязки существующих выборок к единой шкале времени при анализе импульсов. Поскольку запуск инициируется непосредственно по входному сигналу или организуется в процессе его обработки, например анализа в реальном времени или постобработки данных из хранилища, синхронизация может являться частью любого из основных функциональных блоков процесса измерений, показанных на рис. 4.
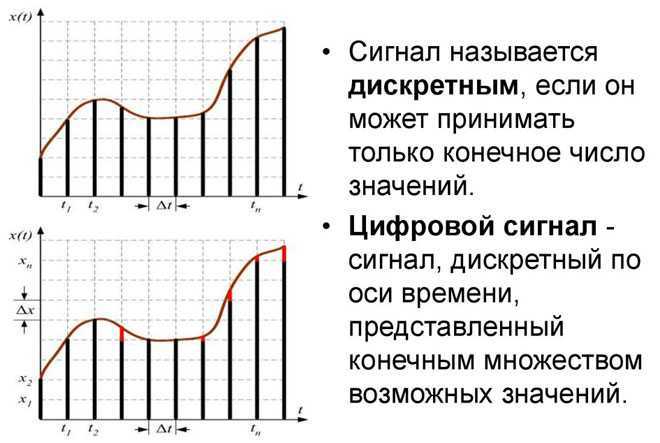
Отличие дискретного сигнала от цифрового
Про Азбуку Морзе наверное слышали все. Придумал художник Самуэль Морзе, другие новаторы усовершенствовали, а использовали все. Это способ передачи текста, где точками и тире закодированы буквы. Упрощенно, кодировка называется морзянкой. Её долго использовали на телеграфе и для передачи информации по радио. Кроме того, сигналить можно с помощью прожектора или фонарика.
Код морзянки зависит только от самого знака. А не от его продолжительности или громкости (силы). Как ни ударь ключом (моргни фонариком), воспринимаются только два варианта– точка и тире. Можно только увеличить скорость передачи. Ни громкость, ни продолжительность в расчёт ни принимаются. Главное, что бы сигнал дошёл.
Так же и цифровой сигнал
Важно закодировать данные с помощью 0 и 1. Получатель должен только разобрать, комбинацию нолей и единиц
Неважно с какой громкостью и какой продолжительностью будет каждый сигнал. Важно получить нолики и единички. Это суть цифровой технологии.
Дискретный сигнал получится если закодировать ещё громкость (яркость) и продолжительность каждой точки и тире, или 0 и 1. В этом случае вариантов кодировки больше, но и путаницы тоже. Громкость и продолжительность можно не разобрать. В этом и разница между цифровым и дискретным сигналами. Цифровой генерируется и воспринимается однозначно, дискретный с вариациями.
Общие рекомендации по оценке качества цифровых каналов
Кабельные операторы, давно работающие с цифровым телевидением и имеющие большой опыт, советуют классифицировать состояние кабельной сети по трехбалльной шкале. Оценка три балла означает, что параметры каналов в сети соответствуют требованиям качественного приема и обладают достаточным запасом для стабильной, долговременной работы. От оператора при этом требуется только продолжение текущего контроля. Оценка два балла: параметры каналов также соответствуют требованиям качественного приема, но их значения не имеют достаточного запаса для обеспечения долговременной стабильной работы.
Такое состояние сети требует от оператора планового проведения работ для выявления источника проблем и принятия решения о методах восстановления состояния сети до трех баллов. И, наконец, третье состояние сети с оценкой один балл: параметры одного или нескольких каналов не отвечают требованиям качественного приема, что требует от оператора немедленных действий по ремонту или настраиванию сети для поднятия до второго или третьего уровня. Для оценки каждого канала необходимо измерить все параметры на абонентском отводе. Оценка присваивается в соответствии со следующими условиями.
Оценка 3 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: не меньше 36 дБ для модуляции QAM-256 и 28 дБ для модуляции QAM-64.
PreBER не превышает 1E7. PostBER: не превышает 1E9.
Оценка 2 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: находится в пределах от 34 до 36 дБ для модуляции QAM256 и от 26 до 28 дБ для модуляции QAM64.
PreBER: не превышает 1E6. PostBER: не превышает 1E9.
Оценка 1 балл (выполняется хотя бы одно условие):
Уровень канала: не соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.
MER: значение меньше 34 дБ для модуляции QAM-256 и меньше 26 дБ для модуляции QAM-64.
PreBER: значение выше 1E6. PostBER: значение выше 1E-9.
Если есть возможность контроля констелляционной диаграммы, необходимо добавить еще одно условие. Для оценки «3» форма констелляционной диаграммы не должна содержать ярко выраженных фазовых искажений, дисбаланса квадратур и искажений типа компрессии сигнала. При наличии подобных искажений измеряемому каналу должна быть присвоена оценка не выше двух баллов.
При указании значений параметров я исходил из предположения, что они измерены корректно, в пределах погрешности измерения прибора. Но при определенных условиях измеренные значения могут выпадать за пределы погрешности. В этом случае каналу может быть присвоена оценка, не соответствующая действительности.
Данная методика оценки качества не является, конечно, абсолютной и единственно верной. Каждый оператор может для себя выбрать границы значений параметров для оценки качества сигнала в соответствии с особенностями конкретной сети и отдельных каналов; при этом следует придерживаться общего подхода к методу проверки состояния сети.
——
1 Физический смысл этого параметра и формула для вычисления его среднеквадратичного значения рассмотрены в статьях серии «Цифровое кабельное ТВ. Часть 2. Состав головной станции, расчет ретранслируемого потока», «ТелеСпутник», ноябрь 2007 и «Цифровое кабельное ТВ. Часть 4. Сигнал DVB в распределительной сети. Использование альтернативных стандартов», январь 2008 (прим. ред.).
2 I= A cosφ, а Q = A sinφ где А – амплитуда QAM символа, а φ – фаза символа.
3 Имеется в виду мощностная характеристика, в качестве которой в телевидении принято использовать эквивалентное напряжение немодулированного сигнала, который по мощности равен сигналу телевизионному. Хотя в статье применяется термин «мощность цифрового канала», на самом деле подразумевается как раз напряжение этого эквивалентного сигнала (прим. автора).
4 Полоса измерения определяется полосой пропускания измерительного фильтра (прим. ред.).
5 Так эта формула выглядит в ГОСТ Р 52023 (прим. автора).
6 Коэффициент зависит в основном от параметров детектора (тип детектора и его постоянные времени) и прямоугольности измерительного фильтра. Определяется опытным путем и, как правило, составляет 13 дБ (прим. автора).
Андрей Конорев,
ведущий инженер ООО «Планар»
Как проверить ресивер спутниковой антенны
Перед тем как приступить к следующей попытке проверить антенну, лучше ещё раз попробовать предыдущие этапы. Возможно, где-то была допущена ошибка. Если же ничего не помогает можно проверить ресивер на исправность.
- Сначала следует зайти в ручные настройки и записать параметры для спутника этого провайдера.
- Затем, взять устройство и подключить к другому спутниковому телевидению.
- После чего, в меню выбрать ручной поиск, где найти нужный спутник и выставить уже записанные параметры.
- Если обе шкалы цветные и в числовом значении, значит, ресивер исправен, иначе его придётся сдать в ремонт.
В любом случае не стоит сразу же кидаться и покупать неисправный элемент или вызывать мастера. Лучше попытаться пройтись по каждому пункту проверки телевизионной антенны 2–3 раза. И только тогда можно делать какие-то выводы.
Виды сигналов
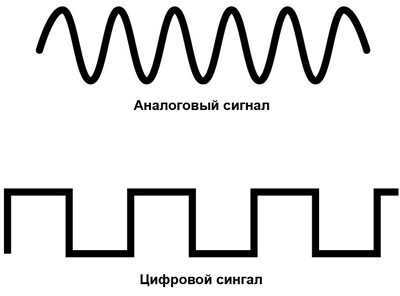
Сигнал это изменение физической величины во времени и пространстве. По сути это коды для обмена данными в информационной и управленческой средах. Графически любой сигнал можно представить в виде функции. По линии на графике можно определить тип и характеристики сигнала. Аналоговый будет выглядеть как непрерывная кривая, цифровой как ломаная прямоугольная линия, скачущая от ноля до единицы. Все, что мы видим глазами и слышим ушами поступает в виде аналогового сигнала.
Аналоговый сигнал
Зрение, слух, вкус, запах и тактильные ощущения поступают нам в виде аналогового сигнала. Мозг командует органами и получает от них информацию в аналоговом виде. В природе вся информация передаётся только так.
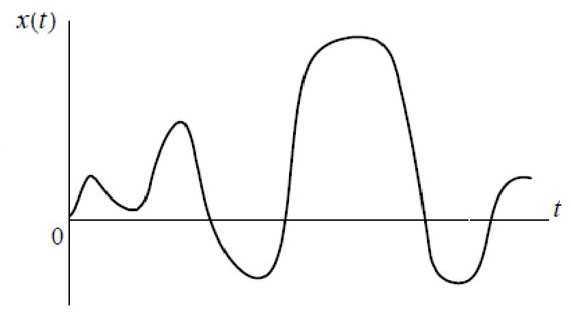
В электронике аналоговый сигнал основан на передаче электричества. Определённым величинам напряжения соответствуют частота и амплитуда звука, цвет и яркость света изображения и так далее. То есть цвет, звук или информация являются аналогом электрического напряжения.
При этом неважно идёт сигнал по проводам или радио. Передатчик непрерывно отправляет, а приёмник обрабатывает аналоговый вид информации
Принимая непрерывный электрический сигнал по проводам или радиосигнал через эфир приёмник преобразует напряжение в соответствующий звук или цвет. Изображение появляется на экране или звук транслируется через динамик.
Дискретный сигнал
Вся суть кроется в названии. Дискретный от латинского discretus, что означает прерывистый (разделённый). Можно сказать, что дискретный повторяет амплитуду аналогового, но плавная кривая превращается в ступенчатую. Изменяясь либо во времени, оставаясь непрерывной по величине, или по уровню, не прерываясь по времени.
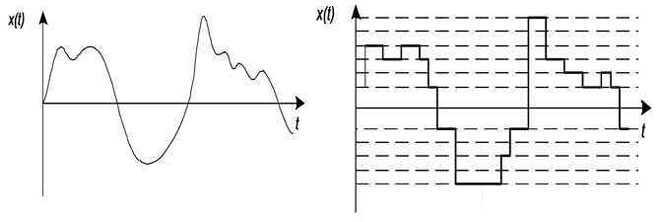
Так, в определенный период времени (например миллисекунду или секунду) дискретный сигнал будет какой-то установленной величины. По окончании этого времени он резко изменится в большую или меньшую сторону и останется таким ещё миллисекунду или секунду. И так беспрерывно. Поэтому дискретный это преобразованный аналоговый. То есть полпути до цифрового.
Цифровой сигнал
После дискретного следующим шагом преобразования аналогового стал цифровой сигнал. Главная особенность – либо он есть, или его нет. Вся информация преобразуется в сигналы ограниченные по времени и по величине. Сигналы цифровой технологии передачи данных кодируются нолем и единицей в разных вариантах. А основой является бит, принимающий одно из этих значений. Бит от английского binarydigit или двоичный разряд.
Но один бит имеет ограниченную возможность для передачи информации, поэтому их объединили в блоки. Чем больше битов в одном блоке, тем больше информации он несёт. В цифровых технологиях используют биты объединенные в блоки кратные 8. Восьмибитовый блок назвали байтом. Один байт небольшая величина, но уже может хранить зашифрованную информацию о всех буквах алфавита. Однако при добавлении всего одного бита число комбинаций ноля и единицы удваивается. И если 8 битов делает возможным 256 вариантов кодировки, то 16 уже 65536. А килобайт или 1024 байт и вовсе немаленькая величина.
В большом количестве объединённых байтов хранится много информации, чем больше комбинаций 1 и 0 тем больше закодировано. Поэтому в 5 – 10 МБ (5000 – 10000 кБ) имеем данные музыкального трека хорошего качества. Идём дальше, и в 1000 МБ закодирован уже фильм.
Но так как вся окружающая людей информация аналоговая, то для её приведения в цифровой вид нужны усилия и какое-либо устройство. Для этих целей был создан DSP (digital signal processor) или ЦПОС (цифровой процессор обработки сигналов). Такой процессор есть в каждом цифровом устройстве. Первые появились еще в 70-е годы прошлого века. Методы и алгоритмы меняются и совершенствуются, но принцип остаётся постоянным – преобразование аналоговых данных в цифровые.
Обработка и передача цифрового сигнала зависит от характеристик процессора — разрядности и скорости. Чем они выше, тем качественней получится сигнал. Скорость указывается в миллионах инструкций в секунду (MIPS), и у хороших процессоров достигает нескольких десятков MIPS. Скорость определяет сколько единиц и нолей сможет устройство «запихнуть» в одну секунду и качественно передать непрерывную кривую аналогового сигнала. От этого зависит реалистичность картинки в телевизоре и звука из динамиков.
Проверка TV сигнала без телевизора
Методика измерения уровня телевизионного сигнала без использования бытовых приборов, заключается в подключении соответствующей аппаратуры в цепь между антенной и ресивером, либо напрямую к антенному кабелю. Таким методом измерительное устройство фиксирует уровень входного сигнала, и специалист определяет его параметры. В соответствии с полученными результатами, настраивается встроенный приемный блок телевизора или же отдельно подключенного ресивера. Специалисту в этом случае, остается только правильно сориентировать приемную антенну и согласовать ее параметры с паспортными характеристиками приемной аппаратуры. Обычно антенну направляют таким образом, чтобы получить максимальный уровень TV сигнала.
Современные приборы для настройки стандартных и спутниковых антенн на сегодняшний день представлены в весьма широком ассортименте. К ним можно отнести:
- измерители уровня телевизионного сигнала со стрелочной или цифровой индикацией;
- приборы с встроенным компасом, определяющим положение спутника;
- устройства с собственным программным обеспечением и возможностью ввода дополнительных параметров настройки;
- спектроанализаторы, использующиеся для более тонкой и точной настройки принимающей аппаратуры;
- универсальные анализаторы, работающие в режиме TV приемника с поддержкой различных форматов изображения.
Выбор вида измерительной аппаратуры напрямую зависит от типа антенны и задач, которые ставятся перед специалистом.
