Парадоксальные фигуры [1972 грегори р.л.

Апория «Ахиллес и черепаха»

Парадокс Ахиллеса и черепахи — одна из апорий (логически верных, но противоречивых высказываний), сформулированных древнегреческим философом Зеноном Элейским в V-м веке до нашей эры. Суть её в следующем: легендарный герой Ахиллес решил посоревноваться в беге с черепахой. Как известно, черепахи не отличаются прыткостью, поэтому Ахиллес дал сопернику фору в 500 м. Когда черепаха преодолевает эту дистанцию, герой пускается в погоню со скоростью в 10 раз большей, то есть пока черепаха ползёт 50 м, Ахиллес успевает пробежать данные ей 500 м форы. Затем бегун преодолевает следующие 50 м, но черепаха в это время отползает ещё на 5 м, кажется, что Ахиллес вот-вот её догонит, однако соперница всё ещё впереди и пока он бежит 5 м, ей удаётся продвинуться ещё на полметра и так далее. Дистанция между ними бесконечно сокращается, но по идее, герою так и не удаётся догнать медлительную черепаху, она ненамного, но всегда опережает его.

www.student31.ru

Конечно, с точки зрения физики парадокс не имеет смысла — если Ахиллес движется намного быстрее, он в любом случае вырвется вперёд, однако Зенон, в первую очередь, хотел продемонстрировать своими рассуждениями, что идеализированные математические понятия «точка пространства» и «момент времени» не слишком подходят для корректного применения к реальному движению. Апория выявляет расхождение между математически обоснованной идеей, что ненулевые интервалы пространства и времени можно делить бесконечно (поэтому черепаха должна всегда оставаться впереди) и реальностью, в которой герой, конечно, выигрывает гонку.

Аналогия суперпозиции и понятия первичного опыта (вместо заключения)

По ходу чтения, по всей видимости, вам, уважаемый читатель, уже становятся очевидными аналогии между уже устоявшимся в диалогово-феноменологической психотерапии понятием первичного опыта и квантовой категорией когерентной суперпозиции. И то, и другое понятие апеллируют к некоему источнику реальности, не сводясь собственно к самой реальности. И та, и другая категории иррелевантны привычным для нас представлениям о Я, объекте, времени и пространстве. В данной работе в рамках обсуждаемого контекста психотерапии мы вполне могли бы использовать оба термина как взаимозаменяемые. Однако, на мой взгляд, категория первичного опыта в большей степени отражает суть происходящего в психотерапии. Именно по этой причине, а также исходя из желания избежать путаницы психологических и физических терминов, в дальнейшем обсуждении проблем диалогово-феноменологической психотерапии мы будем опираться именно на категорию первичного опыта. Временное заимствование понятия когерентной суперпозиции нам понадобилось для того, чтобы этой аналогией прояснить сущность процессов, происходящих на уровне первичного опыта. В дальнейшем, если мы и будем обращаться к этому понятию, то лишь как к метафоре процессов, происходящих в психическом.

Фигуры

Невозможные фигурыСтатья, дающая общее представление о невозможных фигурах.

Невозможный треугольникИстория открытия одной из основных
невозможных фигур — невозможного
треугольника. Показаны работы, в которых
использован невозможный треугольник.

Невозможный трезубец
История открытия одной из основных
невозможных фигур — невозможного
трезубца.

Невозможная лестницаО фигуре открытой Лайонелом и
Роджером Пенроузами.

Лента Мебиуса

Об известной фигуре, имеющей только одну
поверхность и одну границу.

Бутылка Кляйна
О загадочной фигуре, имеющей только
одну поверхность.

Гиперкуб

Четырехмерный правильный «многогранник»,
состоящий из восьми кубов.

Кольца Борромео

История и области применения колец
Борромео, известной невозможной фигуры

Невозможный магический куб

Необычное продолжение теории магических квадратов

Узел-трилистник

История и художественное использование фигуры узла-трилистника

Звезда Эрцгаммы

История и значение одной из самых древних невозможных фигур — звезды Эрцгаммы.

Спирали

Спирали

Водовороты

Странно, но в оригинальной работе обошли
вниманием целый класс фигур, которые
достаточно часто встречаются в работах
Эшера. Это закрученные в спирали фигуры

В
работе «Спирали» мы видим четыре
закручивающиеся в спираль полоски, которые
постоянно сближаются и постепенно закручиваются
сами в себя, образуя своеобразный тор. Пройдя целый
круг, спираль заходит внутрь самой себя,
образуя тем самым, как бы, спираль второго
порядка — спираль в спирали.

В работе «Водовороты» Эшер объединил
спиралевидную форму и свой излюбленный
художественный прием — регулярное разбиение плоскости
(или мозаику). Здесь рыбы,выплыв из одного
водоворота, попадают во второй и, погружась
в него, постепенно уменьшаются в размерах и
наконец совсем исчезают

Обратите внимание
на постепенно уменьшающуюся в размерах
мозаику. Если мысленно развернуть спираль,
то мы увидим лишь два ряда рыб, плывущих
навстречу друг другу

Но скрученные в
спираль и соответствующим образом
деформированные образы рыб полностью
покрывают некоторую область бесконечной
плоскости.

Сферические спирали

Иной способ представления спирали
использован в работе «Сферические
спирали», где четыре полосы расположены
на поверхности шара, проходя от одного
полюса шара к другому. Похожий путь может
пройти самолет, летящий с северного полюса
земного шара на южный.

Здесь мы привели основные виды спиралей,
использованных Эшером в своих работах.
Различные их модификации можно обнаружить
и на многих других литографиях художника.

Самовоспроизведение и информация

Рисующие руки

В заключение мы рассмотрим аспекты
творчества Эшера, относящиеся к теории
информации и искусственному интеллекту.
Эта область творчества художника широко
освещена во многих статьях и книгах.
Наиболее полное исследование этого вопроса
освещено в книге Дугласа Хофстадтера (Douglas R.
Hofstadter) «Гёдель, Эшер, Бах: Бесконечная
золотая нить» (Godel, Escher, Bach: An Eternal Golden Braid),
выпущенной в 1980 году и награжденной
пулитцеровской премией.

Рыбы и чешуйки

Центральная идея самовоспроизведения,
взятая на вооружение Эшером, обращается к
загадке человеческого сознания и
способности человеческого мозга
обрабатывать информацию так, как не сможет
обработать ни один компьютер. Литографии
«Рисующие руки» и «Рыбы и чешуйки»
используют эту идею разными способами.
Самовоспроизведение является направленным
действием. Руки рисуют друг друга, создавая
самих себя. При этом сами руки и процесс их
самовоспроизведения неразделимы. В работе
«Рыбы и чешуйки» концепция
самовоспроизведения представлена более
функционально, и в данном случае она может
быть названа самоподобием. В этом смысле
данная работа описывает не только рыб, а все
живые организмы, в том числе и человека.
Конечно, мы не состоит из уменьшенных копий
самих себя, но каждая клетка нашего тела
несет в себе информацию обо всем теле в виде
ДНК.

Три сферы II

Углубляясь в изучение
самовоспроизведения,
можно его обнаружить в отражении и
пересечении отражений реального мира.
Такое пересечение встречается во многих
картинах Эшера. Мы рассмотрим лишь один
пример — литографию «Три сферы», на
которой присутствуют три шаровидных тела,
сделанных из разных материалов с различной
отражающей способностью. Эти сферы
отражают друг друга и художника, и комнату,
в которой он работает, и лист бумаги, на
котором он рисует сферы. Хофстадтер в своей
книге написал «… каждая частица мира
содержит в себе весь мир и содержится к во
всех других частицах мира…».

Таким образом, мы заканчиваем тем же, с
чего начали, — автопортретом художника — его
отражением в своей работе.

Заключение

Мы рассмотрели лишь небольшую часть работ
из сотен набросков и литографий и гравюр,
оставшихся после смерти Эшера в 1972 году

Еще
многое будет сказано и уже сказано о
значении и важности его работ. С каждым
годом появляется все больше и больше книг,
где освещается творчество художника,
анализируются различные аспекты его
творчества

Надеемся, что мы заинтересовали
вас творчеством Эшера.

Англоязычный источник статьи
можно найтиhttp://www.mathacademy.com/pr/minitext/escher/

Перевод Влада Алексеева.

Однобалочник, двухбалочник и что-то между

Возникает вопрос, может ли вообще существовать невозможный однобалочник.
На рисунке 8 сверху показан обычный брусок, ниже – брусок у которого оба среза видны,
а внизу брусок, у которого ни одного среза не видно. Два последних – естественно невозможны,
но ГЛАЗ определяет их как бруски, у которых концы срезаны под углом. Поэтому, согласно
нашей классификации, приведенной выше, они не являются невозможными объектами.

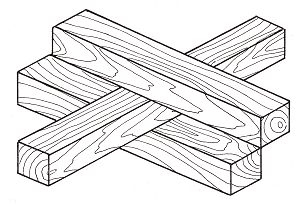Рисунок 7. Бруно Эрнст, «Невозможное проникновение», 1984

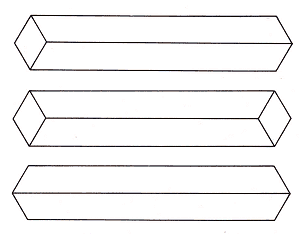Рисунок 8.

В картине Сандро дель Прете
«Врата в четвертое измерение» (рисунок 12) автор, тем не менее,
находит способ составить из таких брусков невозможные объекты путем добавления
дополнительных пространственных деталей. Все четыре бруска направлены от нас,
и из всех объектов, видимых на картине, фигура женщины находится ближе всего к нам.
Все бруски обладают еще одним любопытным свойством: каждая грань бруска одновременно
имеет и горизонтальную и вертикальную ориентацию в зависимости от того, с какой
стороны их рассматривать. Эта особенность подчеркивается надписями на гранях.

На рисунке 7 совершенно нормальный брусок становится невозможным вследствие
своего размещения относительно других брусков: он проходит между двумя другими
брусками, между которыми нет пространства для третьего бруска, так как их ребра
плотно склеены друг с другом.

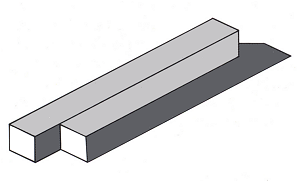Рисунок 9. Зенон Кульпа, «2.5-мерный брусок», 1984

Объект на рисунке 9 был открыт Зеноном Кульпой. На первый взгляд нам кажется,
что мы видим два параллельных бруска, но в правой части один из брусков теряется
в тени своего соседа. Наверное, эту фигуру лучше всего назвать полуторабалочником.

Рисунок 10. Бруно Эрнст «Невозможный двухбалочник»

В случае двухбалочника Эрнста (рисунок 10) прямоугольное сечение в середине
раскрывает двойственную ориентацию фигуры. Фигура выглядит вертикальной на
переднем плане, и горизонтальной – на заднем. Ее интерпретация определяется
пространственной информацией, получаемой от взаимной ориентации концов двух брусков.

Рисунок 11. Сандро дель Прет, «Мировые колеса», рисунок карандашом.

Картина Сандро дель Прете «Cosmic wheels» (рисунок 11) также может
рассматриваться как невозможный (искривленный) двухбалочник. Картина имеет
определенное сходство с работой Эшера «Cube with magic bands» (рисунок 16).

Рисунок 12. Сандро дель Прет, «Врата в четвертое измерение», рисунок карандашом

Математические основы невозможных фигур

Невозможные фигуры в
реальном мире Показаны способы создания невозможный
фигур в реальном мире. Имеются
фотографии невозможных фигур,
раскрывающие их секреты.

Диего Урибе.
Невозможные плитки

Перевод статьи аргентинского ученого
о наборе треугольных плиток, при помощи
которых можно создавать и исследовать
невозможные фигуры.

Корин
Серф. Подкласс невозможных фигур
изучаемый теорией узлов
Рассматривается один из способов
идентификации невозможных фигур
производных от невозможного
треугольника.

Принципы построения
иллюзий
Рассказывается о способах создания и
принципах действия некоторых
классических иллюзий.

Анимация
невозможных фигур Описывается один из способов
создания анимированных невозможных
фигур.

Zenon Kulpa. Наведение
порядка в невозможном
Статья посвящена упорядочению и
классификации невозможных фигур.
Описываются схемы кодирования
мультибаров и линейных фигур.

Кристина Юсупова.
Применение теоремы Эйлера к мультибарамВ статье рассказывается о закономерностях в количестве вершин, ребер и граней
в невозможных мультибарах.

Самоубийство Роналда Опуса

Этот мысленный эксперимент был придуман в 1987 году Доном Харпером Миллсом.

Мужчина попытался покончить жизнь самоубийством, выпрыгнув из окна своей квартиры в многоэтажке. Но как только он прыгнул, в него попала пуля — она вылетела из окна ниже. Стрелял пожилой мужчина — он хотел припугнуть жену ружьем, которое обычно было не заряжено.

В ходе расследования выяснилось, что Роналд Опус, пытавшийся покончить жизнь самоубийством, — сын этого пожилого мужчины. Он тайно зарядил ружье своего отца в надежде, что тот застрелит свою жену (незадолго до инцидента мать перестала оказывать финансовую поддержку своему сыну).

Так что же это: убийство или самоубийство?

Парадокс лестницы (шеста) в специальной теории относительности

Согласно специальной теории относительности, объекты, движущиеся с околосветовой скоростью, .

Представим лестницу, которую вносят в гараж в переднюю дверь и сразу же выносят через заднюю. Длина лестницы на несколько метров больше длины гаража, поэтому ее нельзя хранить в закрытом помещении. Допустим, что лестница движется с околосветовой скоростью по той же траектории, по которой ее вносят в гараж.

За счет лоренцева сжатия длина лестницы относительно гаража должна уменьшиться, поэтому при соответствующей скорости лестница может полностью уместиться в помещении. В этот момент обе двери гаража можно быстро закрыть (чтобы лестница в нем уместилась), а затем открыть (чтобы лестница не ударилась в заднюю дверь гаража).

С другой стороны, если рассмотреть ситуацию из системы отсчета лестницы, то ее длина остается прежней, а длина гаража, напротив, сокращается. Следовательно, в этой ситуации лестница не может полностью уместиться в закрытом гараже. Поскольку обе системы отсчета равноправны, получается парадокс.

Апория «Летящая стрела»

Знаменитый парадокс Зенона Элейского затрагивает глубочайшие противоречия в представлениях учёных о природе движения и времени. Апория сформулирована так: стрела, выпущенная из лука, остаётся неподвижной, так как в любой момент времени она покоится, не совершая перемещения. Если в каждый момент времени стрела покоится, значит она всегда находится в состоянии покоя и не движется вообще, так как нет момента времени, в который стрела перемещается в пространстве.

www.academic.ru

Выдающиеся умы человечества веками пытаются разрешить парадокс летящей стрелы, однако с логической точки зрения он составлен абсолютно верно. Для его опровержения требуется объяснить, каким образом конечный временной отрезок может состоять из бесконечного числа моментов времени — доказать это не удалось даже Аристотелю, убедительно критиковавшему апорию Зенона. Аристотель справедливо указывал, что отрезок времени нельзя считать суммой неких неделимых изолированных моментов, однако многие учёные считают, что его подход не отличается глубиной и не опровергает наличие парадокса. Стоит отметить, что постановкой проблемы летящей стрелы Зенон стремился не опровергнуть возможность движения, как таковую, а выявить противоречия в идеалистических математических концепциях.

Определения

В заключение данной главы давайте попытаемся дать определение невозможным объектам.

В моей первой публикации о картинах с невозможными объектами М.К. Эшера,
которая появилась примерно в 1960 году, я пришел к следующей формулировке:
возможный объект всегда может рассматриваться как проекция — представление
трехмерного объекта. Однако, в случае невозможных объектов, не существует
трехмерного объекта, чьим представлением является данная проекция, и в данном
случае мы можем называть невозможный объект – иллюзорным представлением.
Данное определение является не только неполным, но и неправильным
(к этому мы еще вернемся в главе 7), так как оно относится только математической
стороне невозможных объектов.

Рисунок 23. Oscar Reutersvärd, «Cubic organization of space», раскрашенный рисунок тушью, 29×20.6 cm.
В действительности данное пространство не является заполненным,
так как кубы большего размера не связаны с кубами меньшего размера.

Зенон Кульпа
предлагает следующее определение: изображение невозможного объекта –
это двухмерная фигура, создающее впечатление существующего трехмерного объекта,
причем эта фигура не может существовать так, как мы ее пространственно интерпретируем;
таким образом, любая попытка создать его ведет к (пространственным) противоречиям,
которые отчетливо видны зрителю.

Последнее замечание Кульпы предлагает один практический путь выяснения,
является ли объект невозможным или нет: просто попробуйте создать его
самостоятельно. Вы вскоре увидите, возможно даже до начала конструирования,
что вы не сможете этого сделать.

Я предпочел бы определение, которое подчеркивает, что ГЛАЗ при анализе невозможного
объекта приходит к двум противоречивым заключениям.
Мне больше нравится именно такое определение, так как оно охватывает причину этих взаимно
конфликтующих заключений, и, кроме этого, разъясняет тот факт, что невозможность –
это не математическое свойство фигуры, а свойство интерпретации фигуры зрителем.

На основании этого я предлагаю следующее определение:

Невозможный объект обладает двухмерным представлением, которое ГЛАЗ интерпретирует
как трехмерных объект, причем в то же время ГЛАЗ определяет, что данный
объект не может быть трехмерным, так как пространственная информация,
содержащаяся в фигуре, — противоречива.

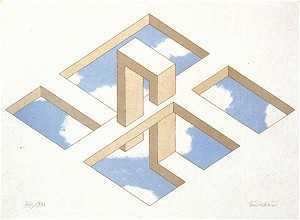Рисунок 24. Oscar Reutersväird, «Impossible four-bar with Crossbars»

Рисунок 25. Bruno Ernst, «Mixed illusions», фотография, 1985

Обманчивое заполнение плоскости невозможными трибарами

На первый взгляд композиция Реутерсварда на

имеет ряд сходств с картиной Эшера «Cubic division of space»,
созданной им в 1952 году. Но, фактически, картина Реутерсварда представляет
сеть невозможных трибаров, в которой большие кубы висят как прозрачный
занавес на переднем плане, никак не связанный с кубами на второй линии.
Те кубы, в свою очередь, выглядят как вторая занавеска позади первой,
за которой следует третья – с еще меньшими кубами.

Hermann Paulsen
использует изогнутую сеть трибаров (рис. 1) для представления
заполнения сферического объема. Уменьшение размеров трибаров ближе к краям создает эффект сферы.

Парадокс Журдена с карточкой

Проблему, предложенную британским логиком и математиком Филиппом Журденом в начале XX-го века, можно считать одной из разновидностей знаменитого парадокса лжеца.

Филипп Журден

Представьте себе — вы держите в руках открытку, на которой написано: «Утверждение на обратной стороне открытки истинно». Перевернув открытку, вы обнаруживаете фразу «Утверждение на другой стороне ложно». Как вы понимаете, противоречие налицо: если первое утверждение правдиво, то второе тоже соответствует действительности, но в таком случае первое должно оказаться ложным. Если же первая сторона открытки лжива, то фразу на второй также нельзя считать истинной, а это значит, первое утверждение опять-таки становится правдой… Ещё более интересный вариант парадокса лжеца — в следующем пункте.

Парадокс девочки и мальчика

Мартин Гарднер / www.post-gazette.com

В теории вероятностей этот парадокс также называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые он был сформулирован американским математиком Мартином Гарднером в одном из номеров журнала «Scientific American». Учёные спорят над парадоксом уже несколько десятилетий и существует несколько способов его разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный вариант.

В семье есть двое детей и точно известно, что один из них — мальчик. Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей существует четыре возможных комбинации полов детей — две девочки, два мальчика, старший мальчик и младшая девочка и наоборот — девочка старшего возраста и мальчик младшего. Первую можно исключить, так как один из детей совершенно точно мальчик, но в таком случае остаются три возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик — один шанс из трёх.

Парадокс мешка картофеля

nieidealne-danie.blogspot.com

Допустим, у некоего фермера имеется мешок картофеля весом ровно 100 кг. Изучив его содержимое, фермер обнаруживает, что мешок хранился в сырости — 99% его массы составляет вода и 1% остальные вещества, содержащиеся в картофеле. Он решает немного высушить картофель, чтобы содержание воды в нём снизилось до 98% и переносит мешок в сухое место. На следующий день оказывается, что, один литр (1 кг) воды действительно испарился, но вес мешка уменьшился со 100 до 50 кг, как такое может быть? Давайте посчитаем — 99% от 100 кг это 99 кг, значит соотношение массы сухого остатка и массы воды изначально было равно 1/99. После сушки вода насчитывает 98% от общей массы мешка, значит соотношение массы сухого остатка к массе воды теперь составляет 1/49. Так как масса остатка не изменилась, оставшаяся вода весит 49 кг.

Конечно, внимательный читатель сразу обнаружит грубейшую математическую ошибку в расчётах — мнимый шуточный «парадокс мешка картофеля» можно считать отличным примером того, как с помощью на первый взгляд «логичных» и «научно подкреплённых» рассуждений можно буквально на пустом месте выстроить теорию, противоречащую здравому смыслу.

Удивительные парадоксы

5. Существует бесконечно длинный «рог», которые имеет конечный объём, но бесконечную площадь поверхности.

Двигаясь навстречу проблеме, появившейся в 17 веке, мы получаем один из многих парадоксов, связанных с геометрией и бесконечностью.

«Рог Гавриила» формируется путём взятия кривой y = 1/х и поворота вокруг горизонтальной оси, как показано на рисунке.

Используя методы исчисления, которые позволяют вычислить площади и объёмы построенных таким образом фигур, можно видеть, что бесконечно длинный рог фактически имеет конечный объём, равный числу пи, но бесконечную площадь поверхности.

Иными словами, в рог поместится определённое количество краски, но для того, чтобы покрыть краской всю его поверхность, потребуется её бесконечное количество.

6. Гетерологическое слово – это слово, которое не описывает себя. А описывает ли себя слово «гетерологический»?

Это один из многих парадоксов, который долго томил умы современных математиков и логиков.

Примером гетерологического слова может быть слово «глагол», которое не является глаголом по сути (в отличие от «существительного», которое является существительным). Другим примером может быть слово «длинный», которое не является длинным словом (в отличие от слова «короткий», которое является коротким словом).

Так «гетерологический» является гетеролигическим словом или нет? Если бы это было бы слово, которое не описывает себя, тогда оно бы описывало себя. А если бы оно было словом, которое описывает себя, оно бы не описывало себя.

Это связано с парадоксом Рассела, который спрашивает, содержит ли определённое множество себя в качестве элемента.

Создавая подобные самоуничтожающиеся множества, Бертран Рассел (Bertrand Russell) и другие учёные продемонстрировали важность установления тщательных правил при создании множеств, которые заложили основу математики 20 века

Невозможные мультибары

На рисунке 22 представлена сплошная рамка, находящаяся выше и левее относительно точки зрения зрителя.
С этого угла каждый угол выглядит по-разному, так что все типы углов можно
пронумеровать цифрами от 1 до 4.

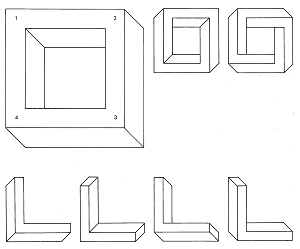Рисунок 22.

Рамка может быть описана данными числами (1234). Используя углы в разных комбинациях,
мы можем построить рамки, в которых ГЛАЗ будет обнаруживать противоречивые пространственные
отношения. Две фигуры в правой части рисунка 22 показывают невозможные четырехбалочники.
Один из них имеет комбинацию углов (4444), второй – (4141).

Используя данный принцип, без труда можно объединить более чем четыре бруска в невозможную фигуру.

Заметим, однако, что мультибары (многобалочники), созданные таким способом, менее
привлекательны в качестве невозможных объектов, чем невозможный трибар и четырехбалочник.
Во-первых, предположение наличия прямых углов в невозможном объекте, то есть расположения
брусков перпендикулярно друг к другу, служит ГЛАЗу отправной точкой для определения
направлений в пространстве, и любые противоречия в данном случае будут более очевидны.
Однако, стороны мультибара всегда соединяются по углом большим, чем 90 градусов, и
направления в пространстве определить сложнее. Во-вторых, чем больше брусков и линий в
объекте, тем менее бросаются в глаза противоречия. Однако, создавать мультибары очень
просто. На рисунке 23 мы видим один пятибалочник (13143), один шестибалочник (444444) и
искривленный двухбалочник (44), с которым мы встречались ранее на рисунке 11.

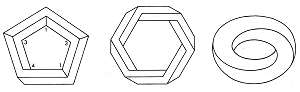Рисунок 23.

Презентация на тему: » Геометрические парадоксы Парадокс-явление, кажущееся невероятным и неожиданным. Геометрические парадоксы основаны на том, что наш мозг всегда пытается.» — Транскрипт:

Геометрические парадоксы Парадокс-явление, кажущееся невероятным и неожиданным. Геометрические парадоксы основаны на том, что наш мозг всегда пытается представить нарисованные на бумаге двухмерные рисунки как трехмерные.

Основные типы геометрических парадоксов «Невозможный треугольник» «Бесконечная лестница» «Космическая вилка» «Сумасшедший ящик»

«Невозможный треугольник» Первую невозможную фигуру изобразил шведский художник Оскар Реутерсвард в 1934 году. Шведское правительство решило увековечить три картины художника на почтовых марках, одной из них стал и невозможный треугольник.

Трибар Трибар – разновидность невозможного треугольника. Его авторы — отец и сын Лайонелл и Роджер Пенроузы, генетик и математик. Трибар появился в 1958 году в журнале British Journal of Psychology, в статье под заголовком «Удивительные фигуры, особый вид оптических иллюзий».

Литография М.Эшера «Водопад» основана на фигуре невозможного треугольника. В этой работе два невозможных треугольника соединены в единую невозможную фигуру. Создается впечатление, что водопад является замкнутой системой, работающей по типу вечного двигателя, нарушая закон сохранения энергии.

«Бесконечная лестница» Эту фигуру называют еще «Вечной лестницей», «Непрерывно восходящей и нисходящей тропой» или «Лестницей Пенроуза» – по имени ее создателей. Впервые эта фигура была опубликована в 1958 году Лайонелом и Роджером Пенроузами в British Journal of Psychology. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.

«Бесконечной лестницей» с успехом воспользовался художник М. Эшер в своей литографии «Восхождение и нисхождение«(1960 году) Вполне узнаваемая «Бесконечная лестница» аккуратно вписана в крышу монастыря. Монахи непрерывно движутся по лестнице в направлении по часовой стрелке и против нее. Они идут навстречу друг другу по невозможному пути. Им так и не удается ни подняться наверх, ни спуститься вниз.

«Космическая вилка» Этот невозможный объект с тремя (или двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Впервые он появился в печати как часть рекламы California Technical Industries 23 марта 1964 года в номере журнала Aviation Week and Space Technology.

«Сумасшедший ящик» «Сумасшедший ящик» – это вывернутый наизнанку каркас куба. Фигуру можно воспринять двояко. Как и многие другие невозможные объекты, «Сумасшедший ящик» основан на неправильных соединениях, допущенных при рисовании.

Непосредственным предшественником «Сумасшедшего ящика» была «невозможная коробка», которую держит сидящий мальчик в знаменитой гравюре М. Эшера «Бельведер» (1958). Предшественником невозможной коробки Эшера был, в свою очередь, куб Неккера.

Куб Неккера был впервые описан в 1832 году швейцарским кристаллографом Льюисом А. Неккером, который заметил, что кристаллы иногда зрительно меняют форму, когда на них смотришь. Он не является невозможным объектом, однако представляет собой фигуру, в, которой параметр глубины может восприниматься неоднозначно. Когда мы вглядываемся в куб, то замечаем, что голубая грань куба находится то на переднем, то на заднем плане.

Имп-Арт – искусство парадоксальных картин Многие известные художники рисовали работы, в основе которых лежали геометрические парадоксы. Эти работы выделяют в отдельное направление изобразительного искусства — «имп-арт», от английских слов impossible («невозможный») и art («искусство»). Художнику требуется определённое мастерство, чтобы убедить зрителя в наличии объёма, перспективы, создать иллюзию пространства в своём произведении. «Рисовать – значит обманывать» – эти слова М.К. Эшера исполнены глубокого смысла. Невозможные фигуры дают почувствовать масштабы этого обмана.

Геометрические парадоксы и психология Очень интересно наблюдать за человеком, рассматривающим невозможный объект, и так же интересно наблюдать за тем, как он пытается понять его

Невозможные объекты важны для психологов, выясняющих, что же привлекает внимание людей

Интересные парадоксы

3. Если вы восстановили корабль, заменив все его деревянные части, это остался тот же корабль?

Ещё один классический парадокс из Древней Греции, «Корабль Тесея» — это парадокс о противоречиях идентичности. Его хорошо описал Плутарх.

Корабль, на котором Тесей и молодёжь Афин возвращались с Крита, имел 30 весёл, которые были сохранены вплоть до времён Димитрия Фалерея. А всё благодаря тому, что когда старые деревянные доски начали разлагаться, их заменили на новые, более крепкие.

Они держались так долго, что этот корабль стал постоянной темой обсуждения среди философов, которые говорили о логике разных вещей, которые изменяются. Одна группа философов говорила, что корабль остался тем же, в то время, как другие философы настаивали, что после замены брёвен, корабль стал другим.

4. Может ли Всемогущий создать скалу, слишком тяжёлую для того, чтобы он сам мог её поднять?

Как может существовать зло, если Бог всемогущ? Как можем мы называть себя свободными, если Бог всеведущ?

Это лишь несколько из многих существующих парадоксов, касающихся применения вопросов логики к божественной теме.

Некоторые люди могут ссылаться на эти парадоксы, объясняя тем самым, почему они не верят в высшее существо. Однако, другие говорят, что они несущественны и по разным причинам не работают.