Криптографические примитивы
В типичной ситуации, когда используется криптография, две стороны (Анна и Виктор) осуществляют связь по незащищенному каналу. Анна и Виктор хотят быть уверены в том, что передаваемые ими данные не могут быть прочитаны даже в случае возможного перехвата. Более того, так как Анна и Виктор находятся в удаленных друг от друга местах, Анна должна быть уверена, что информация, которую она получает от Виктора, не подвергается изменению во время передачи. Также она должна быть уверена в том, что получаемые ею данные действительно исходят от Виктора, а не от кого-то, выдающего себя за него.
Криптография используется для достижения следующих целей:
-
конфиденциальность: защита данных или личной информации пользователя от несанкционированного просмотра;
-
целостность данных: защита данных от несанкционированного изменения;
-
аутентификация: проверка того, что данные исходят действительно от определенного лица;
-
неотрекаемость: ни одна сторона не должна иметь возможность отрицать факт отправки сообщения.
Для достижения этих целей можно использовать алгоритмы и правила, известные как криптографические примитивы, для создания криптографической схемы. В таблице ниже приведены криптографические примитивы и описано их использование.
| Криптографический примитив | Использование |
|---|---|
| Шифрование с закрытым ключом (симметричное шифрование) | Осуществляет преобразование данных с целью предотвращения их просмотра третьей стороной. При таком способе шифрования для шифрования и расшифровки данных используется один общий закрытый ключ. |
| Шифрование с открытым ключом (асимметричное шифрование) | Осуществляет преобразование данных с целью предотвращения их просмотра третьей стороной. При таком способе шифрования для шифрования и расшифровки данных используется набор, состоящий из открытого и закрытого ключей. |
| Создание криптографической подписи | Позволяет проверить, действительно ли данные исходят от конкретного лица, с помощью уникальной цифровой подписи этого лица. Этот процесс также использует хэш-функции. |
| Криптографическое хэширование | Отображает данные любого размера в байтовую последовательность фиксированной длины. Результаты хэширования статистически уникальны; отличающаяся хотя бы одним байтом последовательность не будет преобразована в то же самое значение. |
Хэш-значения
Хэш-алгоритмы преобразуют двоичные последовательности произвольной длины в двоичные последовательности фиксированного меньшего размера, известные как хэш-значения. Хэш-значение является числовым представлением порции данных. Если в хэшированном абзаце текста изменяется хотя бы одна буква, результат хэширования также меняется. Если хэш является криптостойким, его значение значительно изменится. Например, если изменяется один бит сообщения, результат выполнения криптостойкой хэш-функции может отличаться на 50 %. Несколько входных значений могут преобразовываться в один хэш-код. Однако в вычислительном плане немыслимо найти два разных входных набора данных, результаты хэширования которых полностью совпадают.
Две стороны (Анна и Виктор) могут использовать хэш-функцию для проверки целостности сообщений. Им нужно выбрать хэш-алгоритм для подписывания сообщений. Анна будет писать сообщение, а затем создавать его хэш с помощью выбранного алгоритма. Затем стороны могут применять один из указанных ниже вариантов дальнейших действий.
-
Анна отправляет Виктору сообщение с открытым текстом и хэш сообщения (цифровую подпись). Виктор получает сообщение, применяет к нему хэш-алгоритм и сравнивает свое значение хэша со значением, полученным от Анны. Если хэш-значения совпадают, значит, данные не изменялись. Если хэш-значения не совпадают, значит, данные изменялись после создания.
К сожалению, этот способ не позволяет установить подлинность отправителя. Любой человек может выдавать себя за Анну и отправлять сообщения Виктору. Для этого достаточно подписывать сообщения с помощью такого же хэш-алгоритма, и Виктор сможет лишь проверить, соответствует ли сообщение подписи. Это одна из форм атаки «злоумышленник в середине». Дополнительные сведения см. в примере безопасного обмена данными с шифрованием следующего поколения (CNG).
-
Анна отправляет Виктору сообщение с открытым текстом по незащищенному открытому каналу. По защищенному закрытому каналу она оправляет Виктору хэш сообщения. Виктор получает сообщение с открытым текстом, хэширует его и сравнивает хэш со значением, полученным по закрытому каналу. Если хэши совпадают, Виктор может сделать два вывода:
-
сообщение не было изменено;
-
отправитель сообщения подлинный (Анна).
Для того чтобы такая система работала, Анна должна скрывать оригинальное хэш-значение от всех, кроме Виктора.
-
-
Анна по незащищенному открытому каналу отправляет Виктору сообщение в виде открытого текста, а хэш сообщения помещает на свой общедоступный веб-сайт.
Такой подход позволяет защититься от изменения хэша третьей стороной. Хотя сообщение и его хэш могут видеть все, изменить хэш может только Анна. Злоумышленнику, который хочет выдать себя за Анну, потребуется доступ к её веб-сайту.
Ни один из описанных выше способов не защищает Анну от чтения ее сообщений третьими лицами, так как сообщения передаются в виде открытого текста. Для обеспечения полной защиты обычно требуется использовать цифровые подписи и шифрование.
.NET предоставляет следующие классы, реализующие алгоритмы хэширования:
.NET также предоставляет MD5 и SHA1. Но алгоритмы MD5 и SHA-1 были признаны небезопасными, а теперь рекомендуется SHA-2. SHA-2 включает SHA256, SHA384 и SHA512.
Немного истории
Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом.
К примеру, Алиса зашифровала некоторое сообщение и хочет отправить его Бобу. Естественно, чтобы Боб его прочитал, ему нужен ключ которым было зашифровано данное сообщение. И тут возникает проблема, как передать ключ чтобы его никто не смог перехватить. Пытливые умы предложат — пусть передают при личной встрече, а потом общаются сколько захотят. Да, не спорю, выход. А теперь представьте на секунду, что ваша интернет почта, перед тем как вы авторизируетесь в ней, потребует вашей поездки до физического местоположения сервера с почтой. Удобно? Пожалуй не очень.
Конечно ключ можно передавать по другому каналу связи. Но криптография рассматривает все незащищенные каналы связи как небезопасные. То есть передача ключа Бобу по телефону, например, считается небезопасной так, как ничто не мешает Еве прослушивать и телефон в том числе.
До 70-ых годов, эта проблема настолько стала привычной, что считался аксиомой тот факт, что для передачи сообщения нужно передавать и ключ которым сообщение зашифровано (причем некоторых люди до сих пор считают именно так). Но в 76 году Диффи и Хеллман предложили свой «метод экспоненциального обмена ключей». С этих годов и началось развитие асимметричных криптосистем.
Сеть Фейстеля
Теперь мы готовы перейти к очень важной теме, которая открывает дверь в бескрайний мир современных систем шифрования. Сеть Фейстеля — это метод блочного шифрования, разработанный Хорстом Фейстелем в лаборатории IBM в 1971 году
Сегодня сеть Фейстеля лежит в основе большого количества криптографических протоколов. Попробуем разобрать «на пальцах», что же она собой представляет.
Сеть Фейстеля оперирует блоками открытого текста, поэтому мы рассмотрим механизм ее работы на одном из блоков. С остальными блоками действия будут аналогичны.
- Блок разбивается на две равные части — левую (L) и правую (R).
- После разбиения левый подблок изменяется функцией f с использованием ключа K: . В качестве функции можно представить себе какое угодно преобразование — например, старый добрый шифр сдвига с ключом K.
- Полученный подблок складывается по модулю 2 с правым подблоком R, который до этого был не у дел: .
- Далее полученные части меняются местами и склеиваются.
Как видишь, все достаточно просто. Для того чтобы понять, как это работает, посмотри на схему:
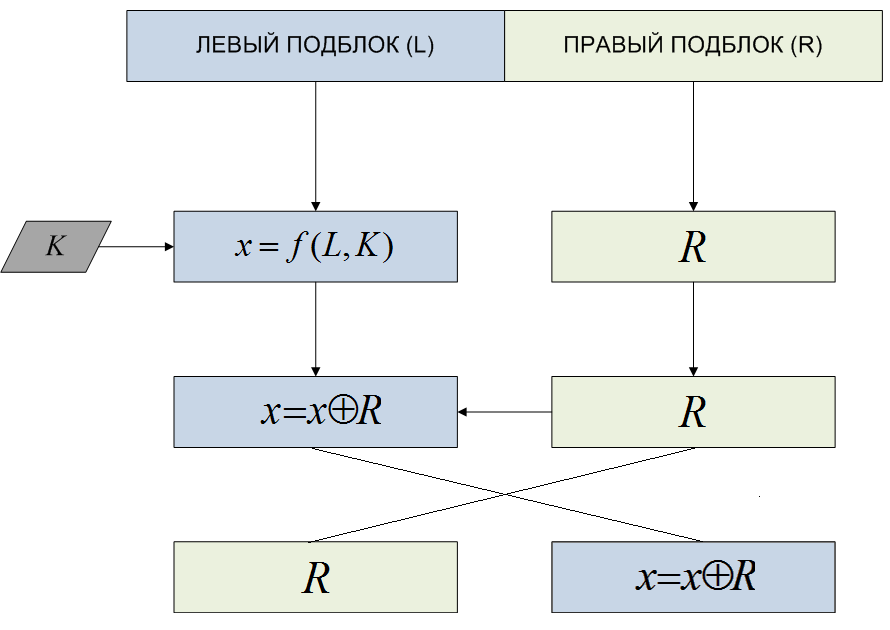 Ячейка Фейстеля
Ячейка Фейстеля
Другие статьи в выпуске:
Xakep #207. Дистанционное банковское ограбление
- Содержание выпуска
- Подписка на «Хакер»-60%
Такая схема называется ячейкой Фейстеля. Сама сеть Фейстеля состоит из нескольких ячеек. Полученные на выходе первой ячейки подблоки поступают на вход второй ячейки, результирующие подблоки из второй ячейки попадают на вход третьей ячейки и так далее в зависимости от количества раундов сети Фейстеля. В каждом таком раунде применяется заранее определенный раундовый ключ. Чаще всего раундовые ключи выработаны из основного секретного ключа K. Когда все раунды будут пройдены, подблоки текста склеиваются, и получается нормальный такой шифротекст.
Теперь посмотрим работу сети Фейстеля на примере. Возьмем слово AVADAKEDAVRA и разобьем его на два блока по шесть символов — AVADAK | EDAVRA. За функцию возьмем шифр сдвига на число позиций, определенных раундовым ключом. Пусть секретный ключ . В качестве раундовых ключей возьмем . Для сложения по модулю 2 переведем текст в двоичный код согласно телеграфному алфавитику, которым вряд ли кто-то еще пользуется вообще.
Вот что получилось:
| A | V | A | D | A | K | E | D | A | V | R | A |
| 00011 | 11110 | 00011 | 01001 | 00011 | 01111 | 00001 | 01001 | 00011 | 11110 | 01010 | 00011 |
Теперь прогоним через сеть Фейстеля из двух раундов первый блок:
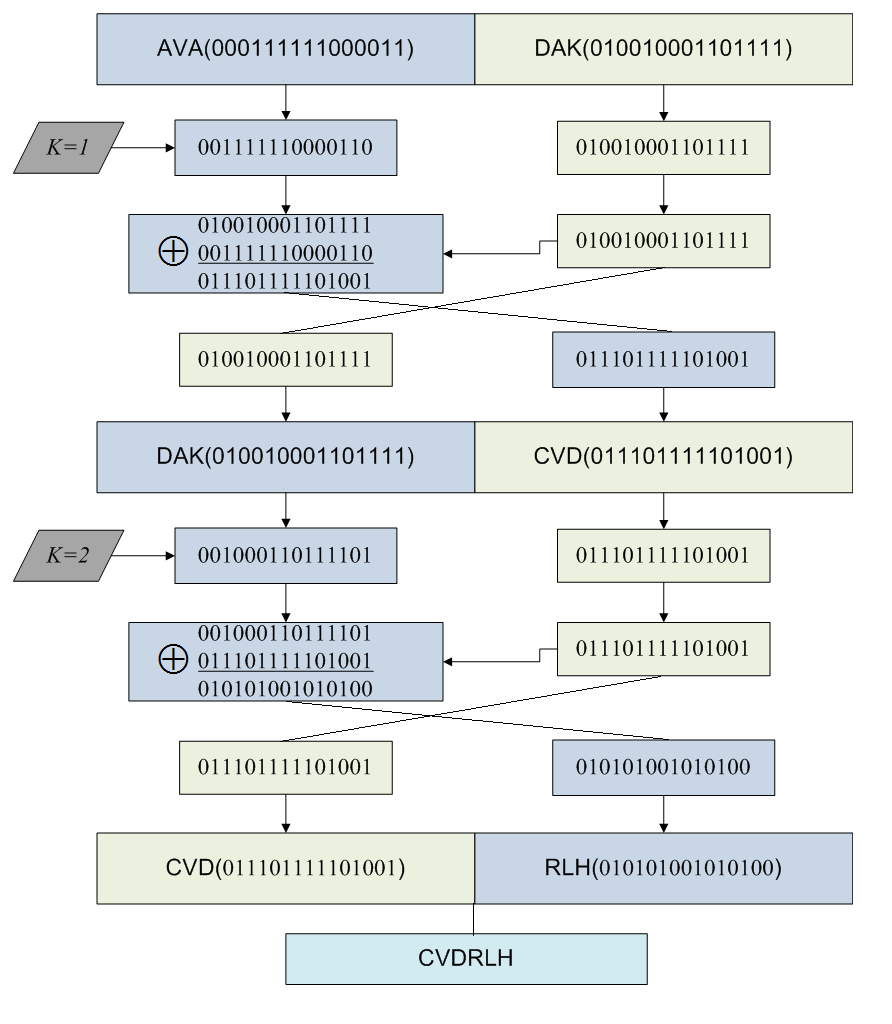 Прогон первого блока
Прогон первого блока
Второй блок попробуй зашифровать сам, у меня получилось MOSSTR.
Расшифрование осуществляется точно так же: шифротекст разбивается на блоки и затем подблоки, левый подблок поступает в функцию, складывается по модулю 2 с правым, и затем подблоки меняются местами. Отличие заключается в том, что раундовые ключи подаются в обратном порядке, то есть в нашем случае в первом раунде применим ключ K = 2, а затем во втором раунде K = 1.
Исследования сети Фейстеля показали, что при независимых раундовых ключах и криптостойкой псевдослучайной функции f трех раундов сети Фейстеля будет достаточно, чтобы шифротекст был псевдослучайным. Это говорит о том, что шифры, основанные на сети Фейстеля, на данный момент достаточно криптостойки.
Реализация комбинированной криптосистемы управления распределением
Главным аспектом асимметричных криптосистем с открытым ключом является их потенциально высокая безопасность. Не нужно передавать ключи, убеждаться в их подлинности. Однако такая системы проигрывает в скорости быстродействия относительно симметричных криптосистем с секретным ключом.
Комбинированная реализация асимметричного и симметричного шифрования разрешает устранить главные минусы, которые характерны системам по отдельности. Идея заключается в следующем:
симметричную криптосистему реализуют для шифрования исходного текста, а асимметричную криптосистему с открытым ключом, для шифрования секретного ключа симметричной криптосистемы.
Такой подход также называют схемой электронного цифрового конверта. Рассмотрим на примере. Пользователь А хочет реализовать гибридный метод шифрования для защищенной транспортировки пакета М пользователю В. Алгоритм таков:
- Действия пользователя А:
- Создает (любым способом) сеансовый секретный ключ Ks, который нужен в симметричном шифровании для зашифровывания пакетов
- Шифрует пакет М симметричным алгоритмом на сеансовом секретном ключе Ks
- Зашифровывает асимметричным алгоритмом секретный сеансовый ключ Ks на открытом ключе KB пользователя В
- Отправляет по открытому каналу пользователю В зашифрованный пакет М вместе с зашифрованным сеансовым ключом Ks
- Действия пользователя В(при получении электроннго цифрового конверта):
- расшифровать асимметричным алгоритмом сеансовый ключ Ks с помощью своего секретного ключа KB
- Расшифровать симметричным алгоритмом пакет М с помощью расшифрованного ключа Ks
Действия пользователей показаны на рис.1
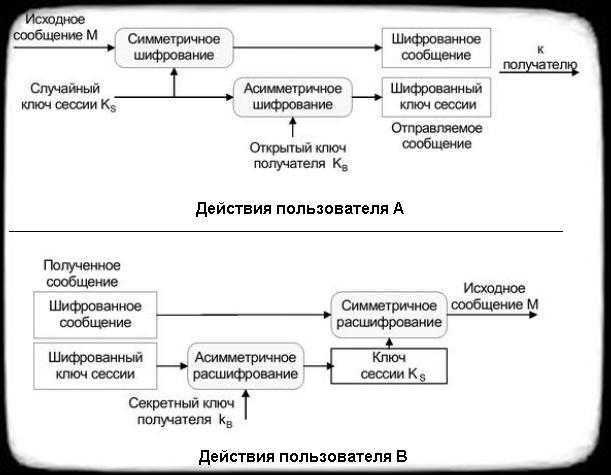 Рисунок — 1
Рисунок — 1
При реализации цифрового конверта минусы асимметричного и симметричного алгоритмов компенсируются из-за:
- проблема распространения ключей симметричного криптоалгоритма устранена тем, что сеансовый ключ Ks передается по открытому каналу в зашифрованном виде с помощью асимметричного криптоалгоритма
- проблема медленной скорости асимметричного алгоритма не уместная, так как шифруется только ключ, а текст шифруется симметричным криптоалгоритмом
Если длина сеансового ключа меньше длины асимметричного ключа, то злоумышленник будет реализовывать атаку на сеансовый ключ. В таблице 1 показано соотношение длин ключей.
Таблица 1 — Длины ключей для асимметричных и симметричных систем при одинаковой криптостойкости
| Длина ключа, симметричной криптосистемы, бит | Длина ключа, асимметричной криптосистемы, бит |
|---|---|
| 56 | 384 |
| 64 | 512 |
| 80 | 768 |
| 112 | 1792 |
| 128 | 2304 |
Блочное шифрование
Зашифруем слово AVADAKEDAVRA. Поскольку шифр блочный, открытый текст разобьем на блоки по четыре символа: AVAD | AKED | AVRA. На практике блоки текста состоят из 64‒256 бит. Для каждого блока придумаем свою таблицу замены:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| b | e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c |
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| p | g | x | e | n | v | c | i | l | h | u | j | b | m | r | s | w | t | k | o | f | d | z | a | y | q |
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| x | w | b | g | s | q | i | v | l | c | u | m | p | o | r | j | t | m | k | n | f | y | h | a | z | d |
А теперь шифруем каждый из блоков соответствующим алфавитом:
|
|
|
Получилось чуть лучше, нежели с поточным подходом, если говорить о стойкости. Ведь обычный шифр замены мы научились дешифровать одной левой. А при таком блочном подходе злоумышленнику придется изрядно поломать голову, прежде чем он сможет подобрать длину блока и уже тогда для каждого блока применить криптоанализ для шифров замены.
Классы криптографии следующего поколения (CNG)
Классы криптографии следующего поколения (CNG) предоставляют управляемую оболочку для собственных функций CNG. (CNG является заменой CryptoAPI.) Эти классы имеют «Cng» в составе их имен. Центральным в группе классов оболочек CNG является класс контейнера ключей CngKey , который абстрагирует хранение и использование ключей CNG. Этот класс позволяет безопасно хранить пару ключей или открытый ключ и ссылаться на него, используя простое строковое имя. Класс цифровых подписей ECDsaCng и класс шифрования ECDiffieHellmanCng на основе эллиптических кривых используют объекты CngKey .
Класс CngKey используется для множества дополнительных операций, включая открытие, создание, удаление и экспорт ключей. Он также предоставляет доступ к базовому дескриптору ключа, используемому при непосредственном вызове собственных функций.
.NET также включает различные вспомогательные классы CNG, такие как:
-
CngProvider поддерживает поставщика хранилища ключей.
-
CngAlgorithm поддерживает алгоритм CNG.
-
CngProperty поддерживает часто используемые свойства ключей.
Другая проблема: если злоумышленник захочет выдать себя за вашего собеседника? anchor link
В нашем примере с Юлией и Сезаром посредники постоянно способны получать метаданные.
Допустим, что один из посредников оказался злоумышленником. Под злоумышленником мы будем подразумевать любого, кто намеревается нанести вам урон, пытаясь украсть либо подменить ваши данные. И по какой-либо причине наш злоумышленник желает узнать о содержимом сообщения Юлии для Сезара.
Допустим, этот злоумышленник смог обмануть Юлию, и она получила подложный файл открытого ключа «Сезара». Юлия не заметила, что это на самом деле не открытый ключ Сезара. Злоумышленник получает сообщение Юлии, просматривает его и передает дальше Сезару.
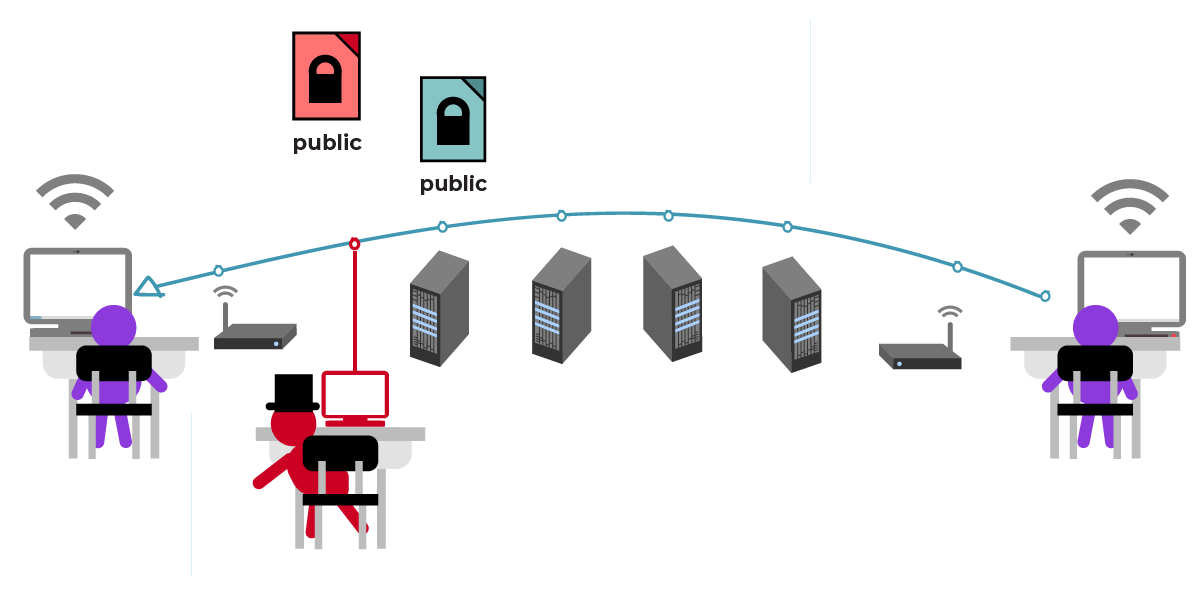
Злоумышленник может даже изменить содержимое сообщения (файла) перед тем, как передать его Сезару.

В большинстве случаев злоумышленник не изменяет содержимое сообщения. Он пересылает сообщение Юлии Сезару как будто бы ничего и не произошло. Сезар узнаёт, что они с Юлией должны встретиться в саду, но к их удивлению там оказывается и злоумышленник.
Это называется «атакой посредника», где посредником может оказаться человек либо компьютер.
К счастью, использование шифрования с открытым ключом способно предотвратить атаку посредника.
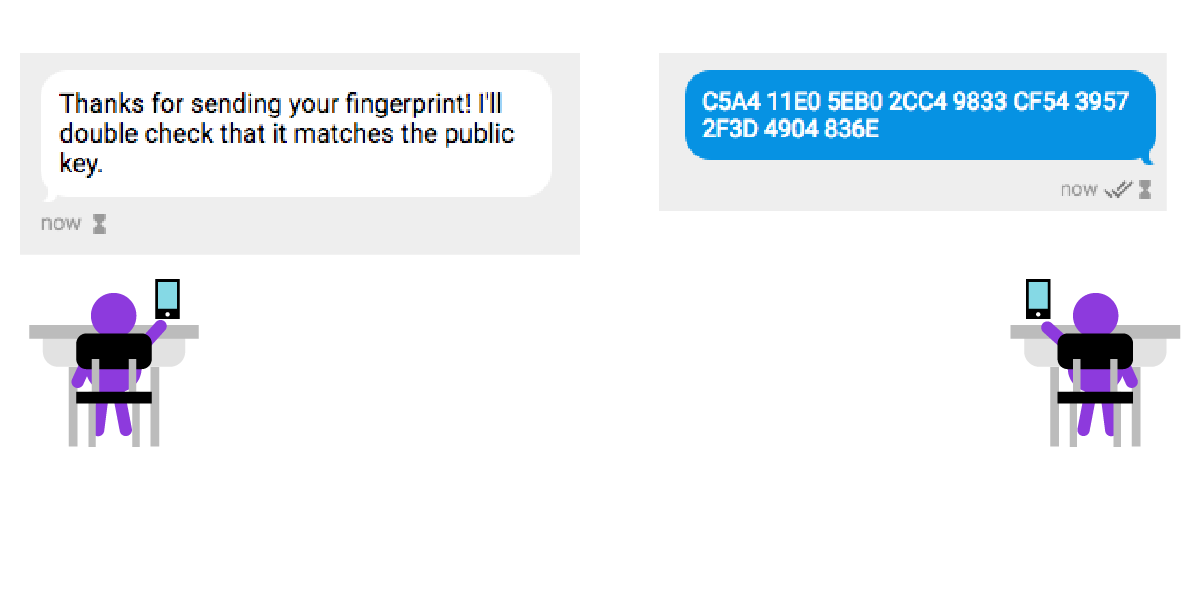
Шифрование с открытым ключом позволяет осуществить двойную проверку соответствия цифрового ключа и личности собеседника посредством так называемой «проверки отпечатков». Лучше всего такую проверку осуществлять при личной встрече. Ваш собеседник сравнит каждый символ отпечатка открытого ключа, предоставленного вами, с отпечатком вашего открытого ключа, находящегося у собеседника. Немного утомительно, но это действительно стоит сделать.
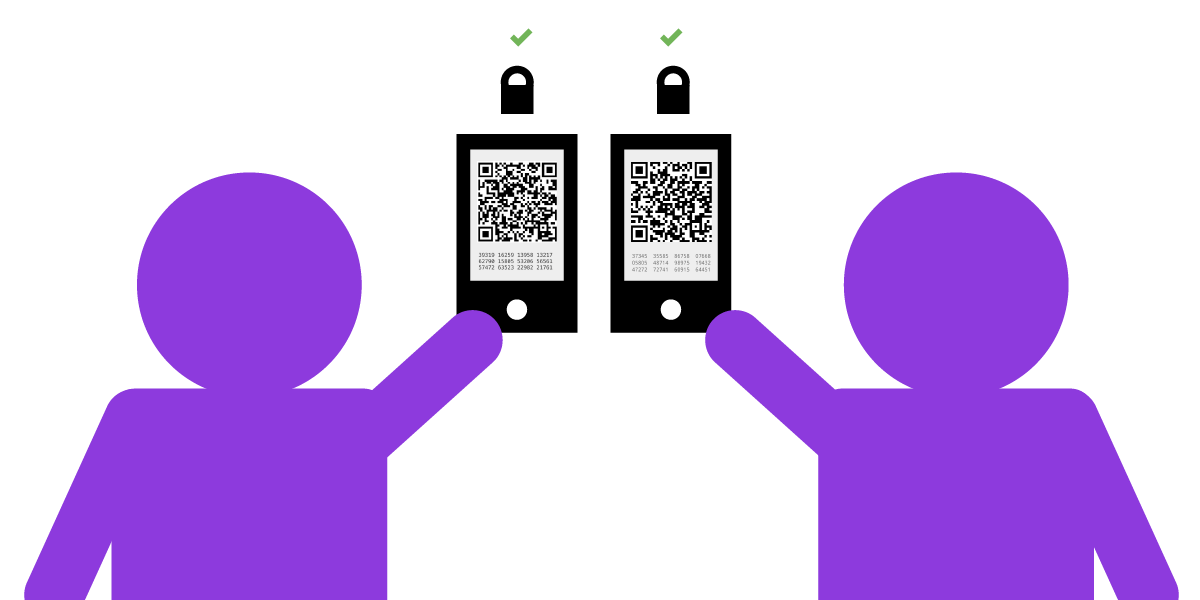
Приложения, использующие сквозное шифрование, также могут проверять отпечатки ключей, хотя и существуют некоторые вариации в названиях и способах реализации. В некоторых случаях необходимо очень внимательно прочитать каждый символ отпечатка, убедившись в том, что отпечаток на вашем экране совпадает с тем, что собеседник видит на своём. Другим способом проверки отпечатка является сканирование QR-кода с экрана телефона собеседника для подтверждения ключа его устройства. В приведённом ниже примере Юлия и Сезар могут встретиться лично, чтобы проверить отпечатки ключей своих телефонов, отсканировав QR-коды друг друга.
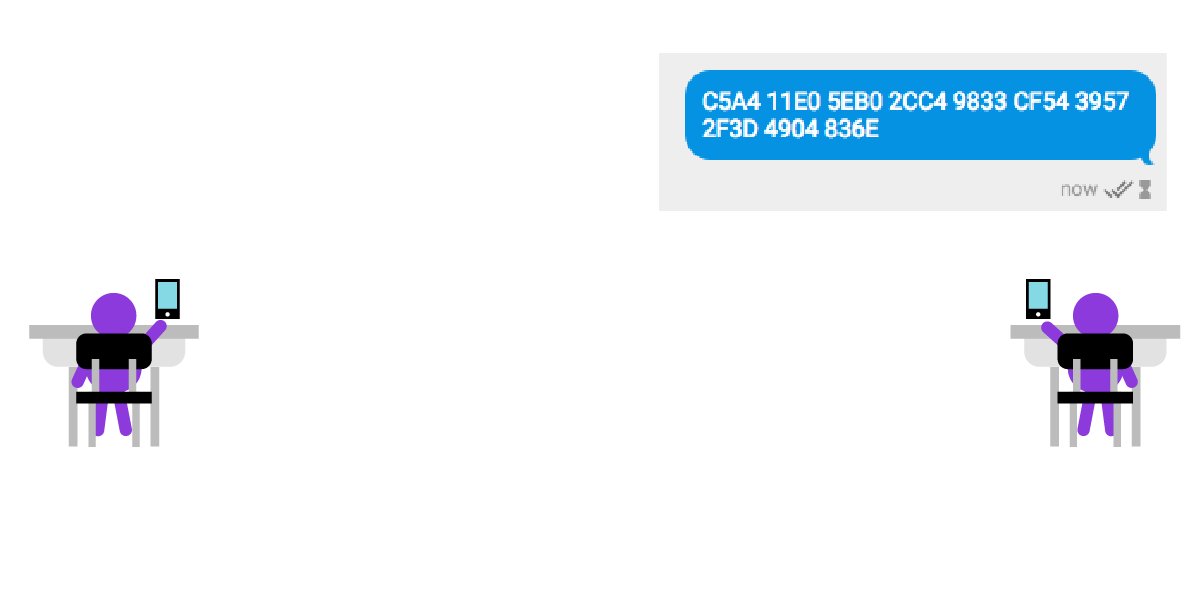
Если же роскошь личной встречи вам недоступна, вы можете отправить свой отпечаток по другому безопасному каналу связи, например с помощью другого мессенджера, чата или HTTPS -сайта, использующего сквозное шифрование.
В данном примере Сезар отправляет отпечаток своего открытого ключа Юлии с помощью смартфона, используя при этом другое приложение со сквозным шифрованием.
Напомним:
- Атака посредника – перехват злоумышленником сообщения, предназначенного вашему собеседнику. Атакующий может внести изменения в это сообщение, а может переслать его дальше, просто ознакомившись с содержимым.
- Криптография (шифрование) с открытым ключом позволяет противостоять атаке посредника с помощью проверки личностей отправителя и получателя. Это делается с помощью проверки отпечатков ключей.
- Открытый ключ вашего собеседника используется для шифрования сообщений, отправляемых ему. У каждого открытого ключа есть сокращенная версия — так называемый «отпечаток открытого ключа». Вы можете использовать его для проверки личности вашего собеседника.
- Закрытый ключ используется для шифрования сообщений в качестве цифровой подписи, подтверждающей ваше авторство.
3. Программы/приложения
Шифрование с открытым ключом в гражданской сфере получило широкое распространение благодаря усилиям американского программиста Фила Зиммермана и его единомышленников. Созданная Филом программа называется PGP (Pretty Good Privacy). Семена дали всходы, была разработана бесплатная программа с открытым кодом GnuPG. Сегодня многие программы используют стандарт OpenPGP. Они совместимы: письмо, зашифрованное одной программой, может быть расшифровано другой программой.
Вашему вниманию предлагается отдельное руководство по Mailvelope.
Ищете что-то еще? Можете попробовать Enigmail. Это дополнение, которое реализует шифрование в популярном офлайновом почтовом клиенте Mozilla Thunderbird. Работает на всех платформах, где способен работать Thunderbird. Если у вас смартфон на Android, можете попробовать «связку» K-9 Mail + OpenKeychain. OpenKeychain «отвечает» собственно за шифрование, а K-9 является почтовой программой. Оба приложения бесплатные и с открытым кодом.
Здесь вы можете посмотреть другие программы.
Версия для печати
Шифрование с открытым ключом: сказание о двух ключах anchor link
Давайте внимательнее рассмотрим ситуацию. Каким образом отправитель передаст получателю симметричный ключ шифрования, исключая возможность того, что злоумышленник может подслушать и эту беседу тоже? В частности, если отправитель и получатель находятся вдали друг от друга, но хотели бы общаться без посторонних?
Криптография с открытым ключом (именуемая также асимметричной криптографией) имеет изящное решение этой проблемы. Шифрование с открытым ключом предполагает создание каждым собеседником пары ключей – открытого ключа (public key) и закрытого ключа (private key). Эти два ключа связаны друг с другом и являются очень большими числами с определёнными математическими свойствами. Если вы зашифруете сообщение, используя открытый ключ собеседника, расшифровать это сообщение можно лишь с помощью соответствующего закрытого ключа.
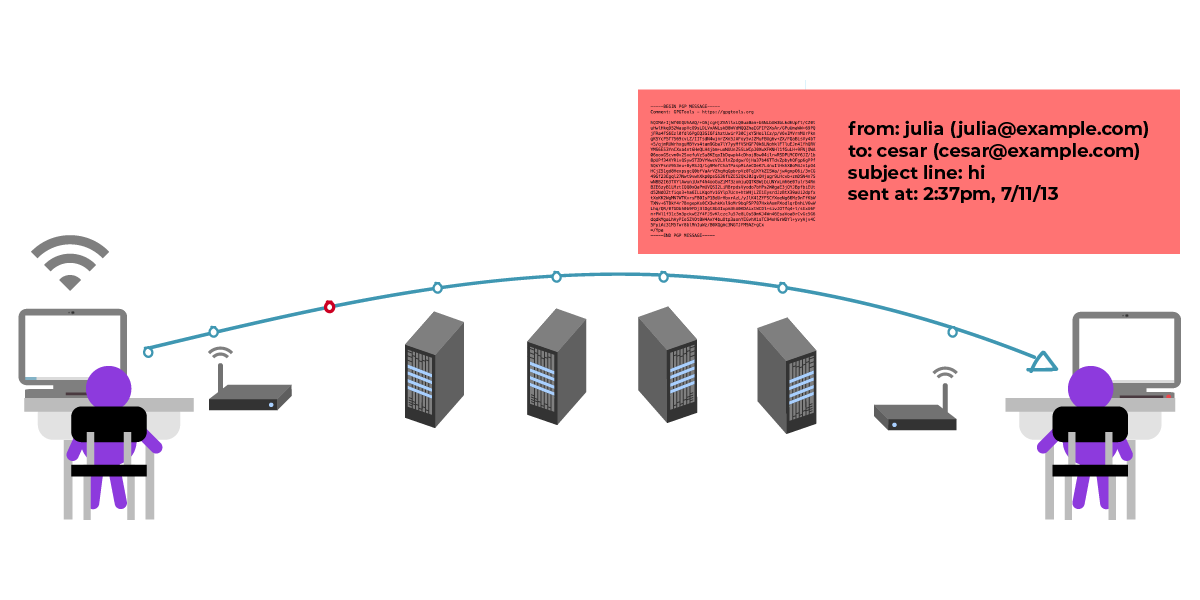
Сейчас вместо передачи записок Юлия и Сезар обмениваются зашифрованными сообщениями через компьютеры, используя при этом открытые ключи шифрования. Их одноклассники, передающие записки с парты на парту, заменены компьютерами. Однако между Юлией и Сезаром есть такие же посредники – их точки доступа Wi-Fi, интернет провайдеры, почтовые сервера. В реальности между Юлией и Сезаром могут находиться сотни компьютеров, обслуживающих их общение. Эти посредники каждый раз делают копии сообщений Юлии и Сезара и хранят их.
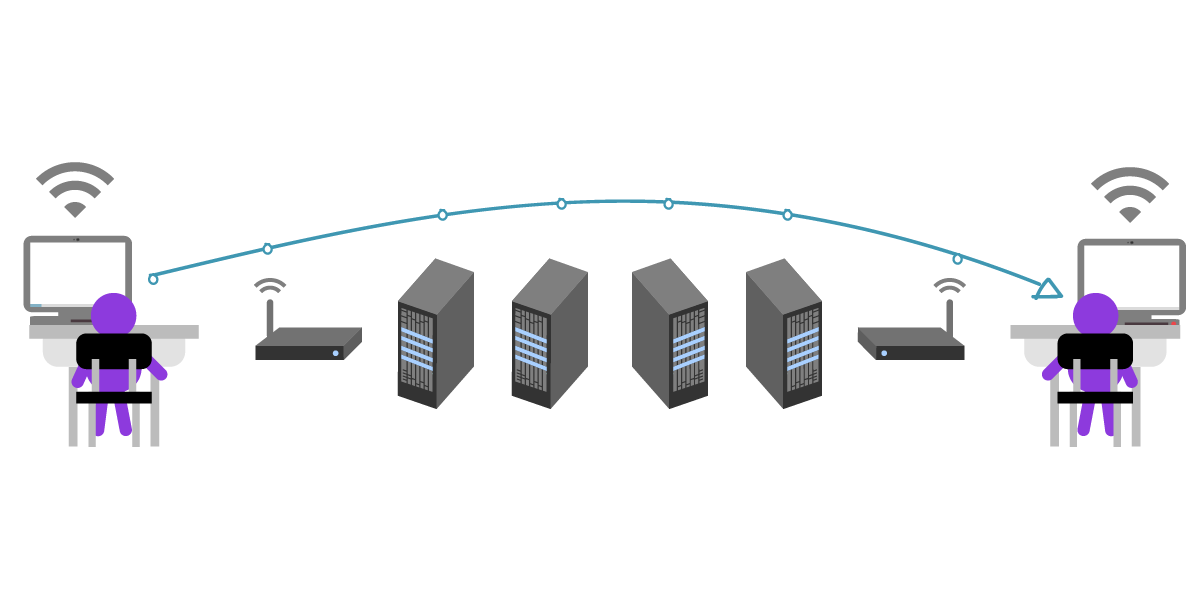
Юлия и Сезар не против того, чтобы посредники знали, что они общаются, но хотели бы оставить содержание своего общения в тайне.
Для начала Юлии необходимо получить открытый ключ Сезара. Он отправляет свой открытый ключ (в виде файла) по незащищённому каналу связи, например в незашифрованном сообщении электронной почты. Он не против того, чтобы посредники получили доступ к его открытому ключу, потому что открытый ключ может свободно распространяться. Имейте в виду, что здесь метафора с ключом перестаёт быть подходящей – не нужно отождествлять открытый ключ с реальным ключом от замка. Сезар отправляет свой открытый ключ по множеству каналов связи, поэтому посредник не сможет подменить его на свой открытый ключ, отправив его Юлии вместо подлинного.
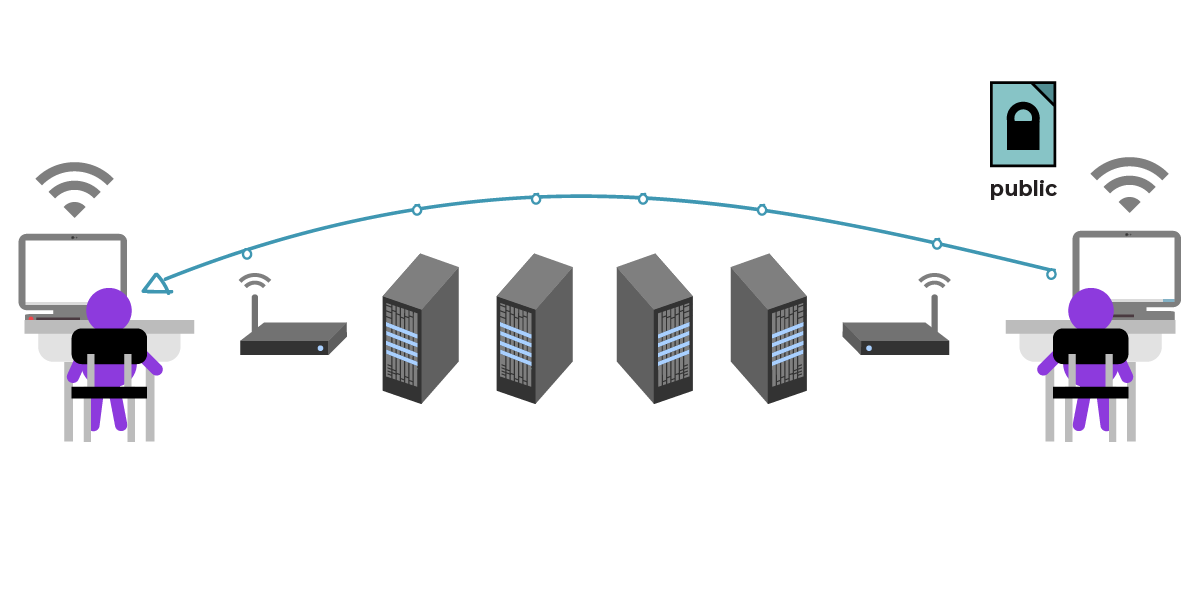
Юлия получает файл, содержащий открытый ключ Сезара. И теперь она может зашифровать своё сообщение Сезару этим ключом! Она пишет в сообщении: «Встретимся в саду».
Она отправляет зашифрованное сообщение. И оно зашифровано лишь для Сезара.
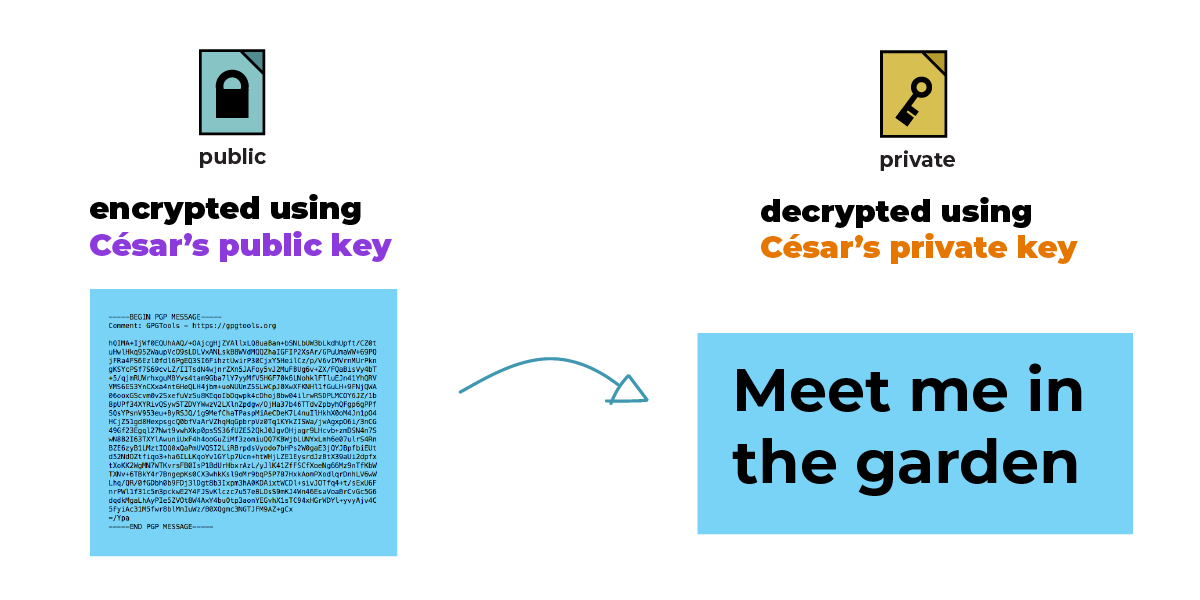
И Юлия и Сезар смогут прочесть сообщение, но для всех остальных оно будет выглядеть как бред. Посредники смогут видеть метаданные письма, например строку «тема», дату и время отправки, адреса отправителя и получателя сообщения.
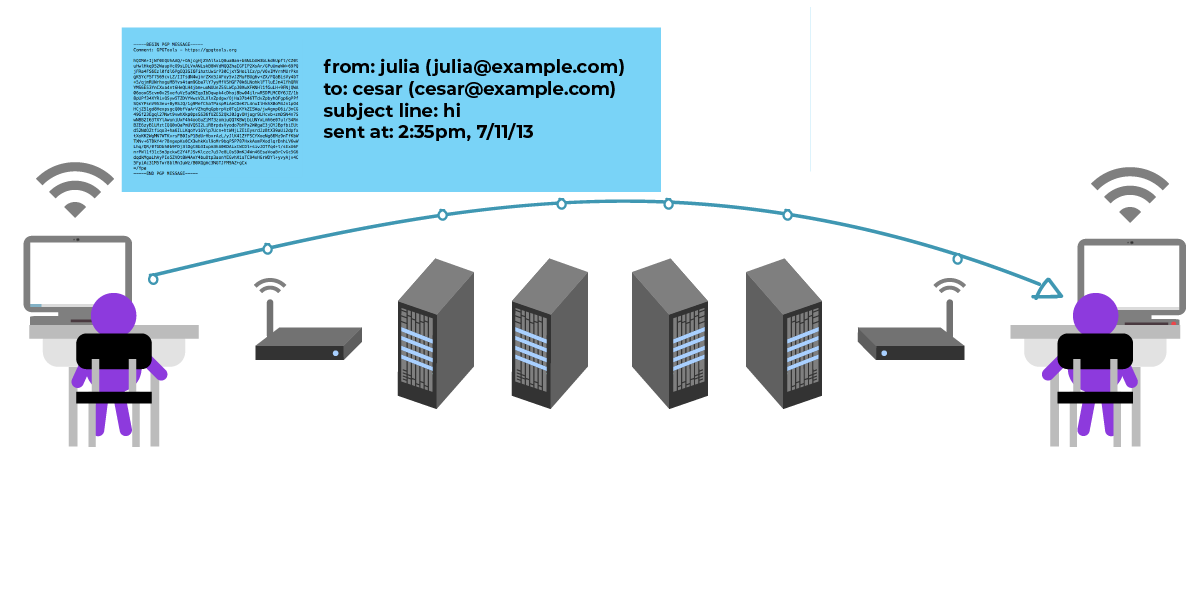
Так как сообщение зашифровано с помощью открытого ключа Сезара, прочитать сообщение смогут лишь сам Сезар и отправитель (Юлия).
Сезар может прочитать это сообщения, используя свой закрытый ключ.

Подведём итог:
- Шифрование (криптография) с открытым ключом позволяет отправить свой открытый ключ по небезопасным каналам связи.
- С помощью имеющегося открытого ключа друга вы сможете зашифровать сообщения для него.
- Ваш закрытый ключ используется для расшифровывания сообщений, зашифрованных с помощью вашего открытого ключа.
- Посредники – такие как сервера электронной почты, интернет провайдеры – могут постоянно видеть метаданные: кто кому отправляет сообщения, когда и в какое время сообщение получено, что содержится в поле «тема», зашифровано ли сообщение и т.д.
Алгоритм Диффи-Хеллмана
И вот однажды Хеллмана осенило и он смог разработать рабочий алгоритм обмена ключами. Для работы по этому алгоритму нужно выполнять шаги на обоих сторонах, поэтому я зарисую это в таблице:
| Алиса | Боб | |
| Этап 1 | Оба участника договариваются о значениях Y и P для общей односторонней функции. Эта информация не является секретной. Допустим были выбраны значения 7 и 11. Общая функция будет выглядеть следующим образом: 7x (mod 11) | |
| Этап 2 | Алиса выбирает случайное число, например 3, хранит его в секрете, обозначим его как число A | Боб выбирает случайное число, например 6, хранит его в секрете, обозначим его как число B |
| Этап 3 | Алиса подставляет число A в общую функцию и вычисляет результат 73 (mod 11) = 343 (mod 11) = 2, обозначает результат этого вычисления как число a | Боб подставляет число B в общую функцию и вычисляет результат 76 (mod 11) = 117649 (mod 11) = 4, обозначает результат этого вычисления как число b |
| Этап 4 | Алиса передает число a Бобу | Боб передает число b Алисе |
| Этап 5 | Алиса получает b от Боба, и вычисляет значение bA (mod 11) = 43 (mod 11) = 64 (mod 11) = 9 | Боб получает a от Алисы, и вычисляет значение aB (mod 11) = 26 (mod 11) = 64 (mod 11) = 9 |
| Этап 6 | Оба участника в итоге получили число 9. Это и будет являться ключом. |
Магия? Не спорю, с первого взгляда непонятно. Но после вчитывания и вдумывания в эту таблицу становится понятно как это работает. Впрочем если понятно не стало, то пролистайте до конца главы, там я выложил поясняющее видео.
Причем обратите внимание, что для получения ключа в конечной формуле, любому человеку нужно иметь три значения:
- Значения a и P, и секретное число Боба B
- или значения b и P, и секретное число Алисы A
Но секретные числа по каналу не передаются! Еве не получится восстановить ключ, не имея чьего-нибудь секретного числа. Почему — я писал выше, данная функция является односторонней. Попробуйте решите уравнение 4x (mod 11) = 2y (mod 11) найдя x и y.
Чтобы было понятнее, как работает схема Хеллмана, представьте шифр, в котором в качестве ключа каким-то образом используется цвет:
Все равно непонятно? Тогда смотрим видео:
https://youtube.com/watch?v=5d8yniGL2G0
Что же, надеюсь, вы поняли, что существует вполне реальный способ безопасного обмена ключами. Но прошу заметить, назвать этот алгоритм асимметричным шифром пока нельзя, так как по сути это всего лишь алгоритм обмена ключами.
Вернемся к математике
Идея с ящиком, о которой я описывал выше, вдохновили Диффи и Хеллмана искать способ передачи сообщения. В конце концов они пришли к использованию односторонних функций.
Что такое односторонняя функция? К примеру есть функция удвоение, т.е удвоить(4)=8, она двухсторонняя, т.к. из результата 8 легко получить исходное значение 4. Односторонняя функция — та функция после применения которой практически невозможно получить исходное значение. К примеру смешивание желтой и синей краски — пример односторонней функции. Смешать их легко, а вот получить обратно исходные компоненты — невозможно. Одна из таких функций в математике — вычисление по модулю.
За основу алгоритма Хеллман предложил функцию Yx (mod P). Обратное преобразование для такой функции очень сложно, и можно сказать что, по сути, заключается в полном переборе исходных значений.
К примеру вам сказали, что 5 x (mod 7) = 2, попробуйте найдите x, а? Нашли? А теперь представьте что за Y и P взяты числа порядка 10300.
Кстати сказать, для повышения стойкости, число P должно являться простым числом, а Y — являться первообразным корнем по модулю P. Но так как мы все же пытаемся понять теорию, то смысла заморачиваться на этом я не вижу.
Теперь пришло время одноключевых КА.
DES
- ECB (англ. electronic code book) — режим «электронной кодовой книги» (простая замена);
- CBC (англ. cipher block chaining) — режим сцепления блоков;
- CFB (англ. cipher feed back) — режим обратной связи по шифротексту;
- OFB (англ. output feed back) — режим обратной связи по выходу.
- Прямым развитием DES в настоящее время является алгоритм Triple DES (3DES). В 3DES шифрование/расшифровка выполняются путём троекратного выполнения алгоритма DES.
RC4
- высокая скорость работы;
- переменный размер ключа.
- используются не случайные или связанные ключи;
- один ключевой поток используется дважды.
Illivion
Blowfish
- скорость (шифрование на 32-битных процессорах происходит за 26 тактов);
- простота (за счёт использования простых операций, уменьшающих вероятность ошибки реализации алгоритма);
- компактность (возможность работать в менее, чем 5 Кбайт памяти);
- настраиваемая безопасность (изменяемая длина ключа).
Twofish
- 128-битный блочный симметричный шифр
- Длина ключей 128, 192 и 256 бит
- Отсутствие слабых ключей
- Эффективная программная (в первую очередь на 32-битных процессорах) и аппаратная реализация
- Гибкость (возможность использования дополнительных длин ключа, использование в поточном шифровании, хэш-функциях и т. д.).
- Простота алгоритма — для возможности его эффективного анализа.
Skipjack
Принимая во внимание, что стоимость вычислительных мощностей уменьшается вдвое каждые 18 месяцев, лишь через 36 лет стоимость взлома Skipjack полным перебором сравняется со стоимостью взлома DES сегодня.
Риск взлома шифра с помощью более быстрых способов, включая дифференциальный криптоанализ, незначителен. Алгоритм не имеет слабых ключей и свойства комплементарности.
Устойчивость Skipjack к криптоанализу не зависит от секретности самого алгоритма.
Mars
- простейшие операции (сложение, вычитание, исключающее или)
- подстановки с использованием таблицы замен
- фиксированный циклический сдвиг
- зависимый от данных циклический сдвиг
- умножение по модулю 232
- ключевое забеливание
Idea
- сложение по модулю
- умножение по модулю
- побитовое исключающее ИЛИ (XOR).
- никакие две из них не удовлетворяют дистрибутивному закону
- никакие две из них не удовлетворяют ассоциативному закону
Режим имитовставки
В этом режиме вырабатывается имитовставка — дополнительный блок фиксированной длины, зависящий от исходного текста и ключей. Такой небольшой блок нужен для подтверждения того, что в шифротекст случайно или преднамеренно не были внесены искажения, — то есть для проверки целостности. Работает этот режим так:
- Блок открытого текста проходит 16 раундов в режиме простой замены.
- К полученному блоку по модулю 2 прибавляется еще один блок открытого текста.
- Сумма проходит еще 16 раундов в режиме простой замены.
- Прибавляется следующий блок открытого текста и опять простая замена и так далее, пока не кончатся блоки открытого текста.
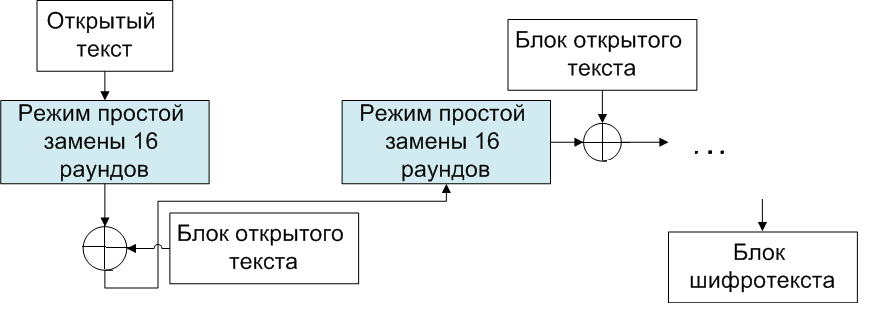 Шифрование в режиме имитовставки
Шифрование в режиме имитовставки
Для проверки получатель после расшифровывания текста проводит аналогичную описанной процедуру. В случае несовпадения результата с переданной имитовставкой все соответствующие M блоков считаются ложными.
Режим простой замены
В режиме простой замены на 32 раунда, согласно стандарту, нам нужно 32 раундовых ключа. Для генерации раундовых ключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: . Ключи являются циклическим повторением ключей . Ключи являются ключами .
- Каждый блок 64 бита делится на два подблока — Ai и Bi.
- Левый подблок Ai складывается по модулю 232 с раундовым ключом K1: .
- Левый подблок проходит через S-бокс.
- Биты левого подблока сдвигаются на 11 позиций (циклический сдвиг).
- Левый подблок складывается с правым по модулю 2: .
- Правый подблок принимает первоначальное значение левого подблока: .
- Подблоки меняются местами.
Сразу пример одного раунда. Ключ 256 бит:
Тогда раундовые ключи
Как пользоваться таким S-боксом? Очень просто! Если на входе S-бокса 0, то на выходе будет 1 (берем 0-й символ S-бокса), если 4, то на выходе будет 5 (берем 4-й символ), если на входе 7, то на выходе 4, и так далее.
Открытый текст:
Входной блок 64 бита
Делится на два 32-битных блока старших и младших битов:
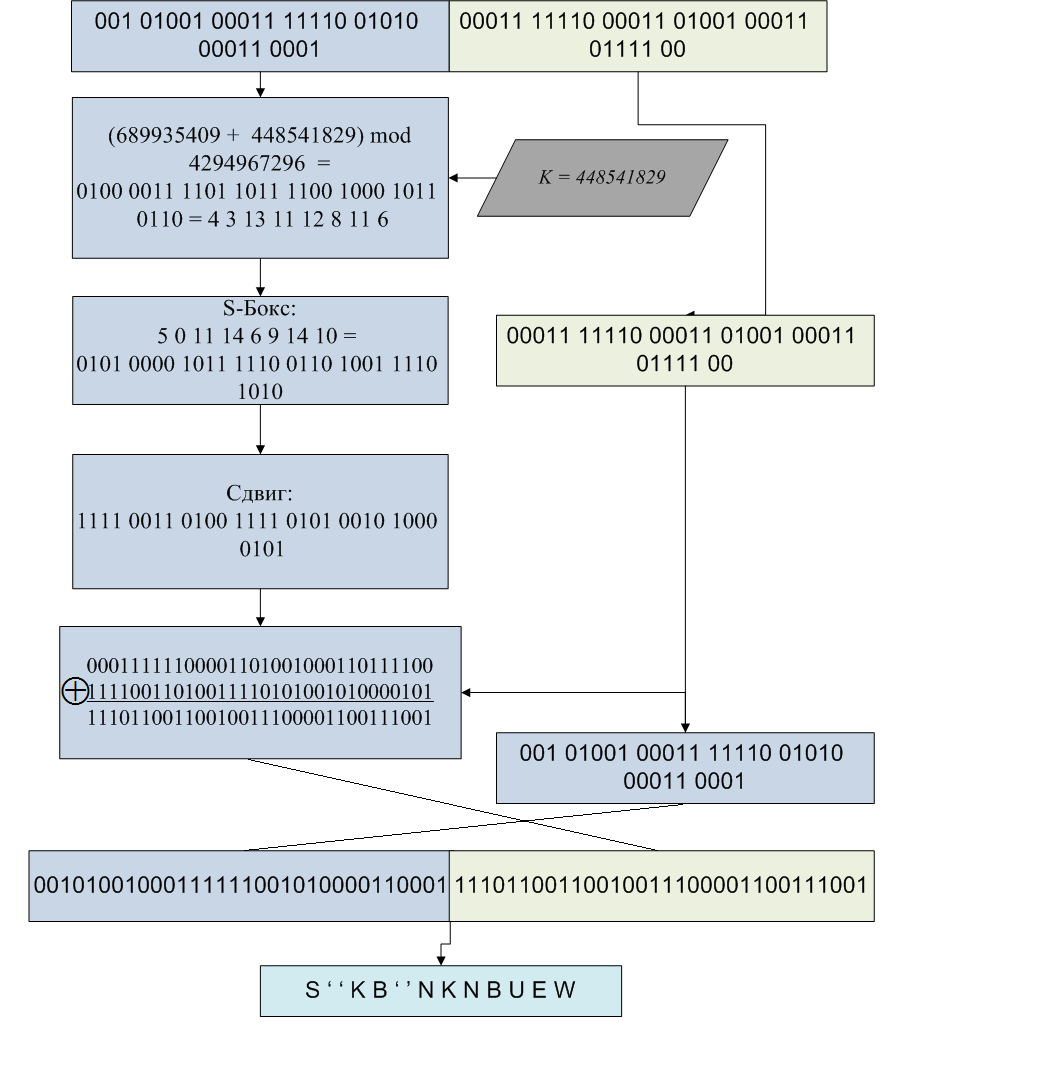 Схема деления на блоки
Схема деления на блоки
Пример, конечно, вышел дикий, потому что ГОСТ — это все-таки не такой стандарт, чтоб каждый мог его ручками перебирать.
Режим простой замены чересчур простой и имеет существенные недостатки:
- одна ошибка в шифрованном блоке искажает все биты этого блока;
- при шифровании одинаковых блоков открытого текста получаются одинаковые блоки шифротекста, что может дать определенную информацию криптоаналитику.
Таким образом, применять ГОСТ 28147—89 в режиме простой замены желательно лишь для шифрования ключевых данных.
Манифесты ClickOnce
Следующие классы шифрования позволяют получать и проверять сведения о подписях манифестов для приложений, развернутых с помощью технологии ClickOnce:
-
Класс ManifestSignatureInformation получает сведения о подписи манифеста при использовании перегрузок его метода VerifySignature .
-
С помощью перечисления ManifestKinds можно указать манифесты, которые нужно проверить. Результатом проверки является одно из значений перечисления SignatureVerificationResult .
-
Класс ManifestSignatureInformationCollection предоставляет коллекцию объектов проверенных подписей ManifestSignatureInformation только для чтения.
Кроме того, перечисленные ниже классы предоставляют сведения о конкретных подписях.
-
StrongNameSignatureInformation содержит сведения о строгом имени подписи для манифеста.
-
AuthenticodeSignatureInformation представляет сведения о подписи Authenticode для манифеста.
-
TimestampInformation содержит сведения о метке времени в подписи Authenticode.
-
TrustStatus предоставляет простой способ проверить, является ли подпись Authenticode достоверной.
2. Шифрование с открытым ключом
Чтобы оставить Захара с носом, Анна (с помощью специальной программы) создает не один, а два ключа. Эти ключи уникальные, парные и обладают особенностью: то, что зашифровано одним ключом, может быть расшифровано только парным ключом. Назовём один из ключей секретным (С), а другой открытым (О). То же самое на своем компьютере сделает Борис. У него появится своя уникальная пара ключей.

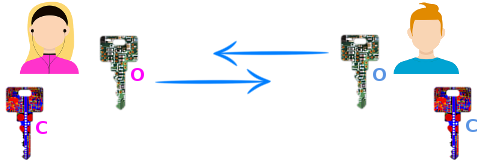
Чтобы написать Борису, Анне нужно:
- сочинить письмо,
- зашифровать его с помощью открытого ключа Бориса,
- отправить шифровку Борису.
Борис:
- получит шифровку,
- расшифрует её с помощью своего секретного ключа (единственного ключа в мире, который это позволит),
- прочтет письмо Анны.
Вот как это выглядит на картинке:
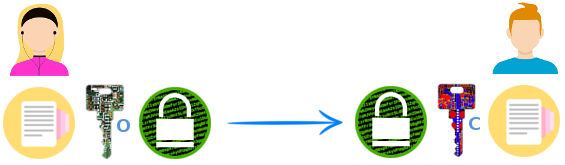
Свой ответ Борис зашифрует открытым ключом Анны. Получив шифровку, Анна расшифрует ее своим секретным ключом.
Что же Захар? Он может перехватывать открытые ключи Анны и Бориса, а также все шифрованные письма. Но никакой пользы это не принесет: открытые ключи не годятся для расшифровки.
Каждый из собеседников может в любой момент создать новую пару ключей, если прежняя потеряна или скомпрометирована.
Немножко реальной жизни
Прежде чем изучать какой либо алгоритм, нужно представить как он работает. И самый простой способ — это сравнить его с работой чего-то в реальности.
И вот начинает казаться что обмен ключами является неизбежной частью шифрования — или все-таки нет?
Представим другую картину. Распишу пошагово:
Значение этой кратенькой истории огромно. Она показывает что два человека могут передавать секретное сообщение без обмена ключами. Вдумайтесь! Эта история фактически рушит все аксиомы на которых была построена тогдашняя криптография. Да мы получаем некоторое усложнение процесса (ящик пришлось пересылать три раза), но результат…
Шифр и ключ anchor link
Вы наверняка сталкивались с чем-либо на первый взгляд непонятным. Это могло быть похоже на надпись на чужом языке или вовсе на какую-то бессмыслицу. Что-то препятствовало прочтению и пониманию. Но это вовсе не означает, что было использовано шифрование.
Каковы отличия чего-то зашифрованного от непонятного?
Шифрование — это математический процесс, используемый для превращения информации в нечитаемый (зашифрованный) вид. При этом восстановление первоначального вида информации (расшифровывание) возможно лишь с помощью специальных знаний. В процессе шифрования используются шифр и ключ.
Шифр — это набор правил (алгоритм), используемый при шифровании и расшифровывании. Это чётко определённые, выраженные в виде формулы правила, которым необходимо следовать.
Ключом является инструкция для шифра: как именно нужно шифровать и расшифровывать данные. Ключи являются одной из наиболее важных концепций в шифровании.