Как лучше обучать rnn для прогнозирования временных рядов?

Скользящее окно для данных временных рядов

Данные временного ряда можно сформулировать как контролируемое обучение.

Учитывая последовательность чисел для набора данных временного ряда, мы можем реструктурировать данные, чтобы они выглядели как контролируемая проблема обучения. Мы можем сделать это, используя предыдущие временные шаги в качестве входных переменных и использовать следующий временной шаг в качестве выходных переменных.

Давайте сделаем это на примере. Представьте, что у нас есть временной ряд следующим образом:

Мы можем реструктурировать этот набор данных временных рядов как контролируемую проблему обучения, используя значение на предыдущем временном шаге, чтобы предсказать значение на следующем временном шаге. Таким образом, реорганизация набора данных временных рядов будет выглядеть следующим образом:

Взгляните на приведенный выше преобразованный набор данных и сравните его с исходным временным рядом. Вот некоторые наблюдения:

• Мы можем видеть, что предыдущий шаг по времени является входом (Икс) и следующий шаг по времени является выходным (Y) в нашей контролируемой проблеме обучения.
• Мы можем видеть, что порядок между наблюдениями сохраняется и должен сохраняться при использовании этого набора данных для обучения контролируемой модели.
• Мы можем видеть, что у нас нет предыдущего значения, которое мы могли бы использовать для предсказания первого значения в последовательности. Мы удалим эту строку, так как не можем ее использовать.
• Мы также можем видеть, что у нас нет известного следующего значения, которое можно было бы предсказать для последнего значения в последовательности. Мы можем захотеть удалить это значение во время обучения нашей контролируемой модели.

Использование предыдущих временных шагов для прогнозирования следующего временного шага называется методом скользящего окна. Для краткости, это может быть названо методом окна в некоторой литературе. В статистике и анализе временных рядов это называется методом отставания или отставания.

Количество предыдущих временных шагов называется шириной окна или размером лага.

Это скользящее окно является основой того, как мы можем превратить любой набор данных временного ряда в контролируемую проблему обучения. Из этого простого примера мы можем заметить несколько вещей:

• Мы можем видеть, как это может работать, чтобы превратить временной ряд в регрессионную или классифицированную задачу обучения под наблюдением для значений реального ряда или маркированных значений временного ряда.
• Мы можем видеть, как после того, как набор данных временного ряда подготовлен таким образом, что любой из стандартных линейных и нелинейных алгоритмов машинного обучения может быть применен, при условии, что порядок строк сохраняется.
• Мы видим, как можно увеличить ширину скользящего окна, чтобы включить больше предыдущих временных шагов.
• Мы можем видеть, как подход со скользящим окном может использоваться для временных рядов, имеющих более одного значения, или так называемых многомерных временных рядов.

Мы рассмотрим некоторые из этих применений скользящего окна, начиная с его использования для обработки временных рядов с более чем одним наблюдением на каждом временном шаге, называемым многомерным временным рядом.

Данные «ПОСЛЕ»

Подобные задачи решаются с использованием датасета, в котором указаны такие признаки, как цена при открытии торгов, цена при закрытии торгов, максимальное значение цены за обозначенный отрезок времени, минимальное значение цены за обозначенный отрезок времени, количество использованных для трейда единиц валюты и время трейда.

Данные были преобразованы в подобный формат и представляли из себя:

time – время трейда

min – минимальное значение цены за обозначенный отрезок времени

max – максимальное значение цены на обозначенный отрезок времени

close – цена при закрытии торгов

Данные, подготовленные для задачи предсказания

Задача предсказания строится таким образом, что при обучении модели признаками x требуется предсказать результат y+1.

Признаками x являются признаки time, max и min. Признаком y является признак close.

Но это не конец

Было бы как-то очень слабо закончить статью на этом месте. Добавлю подводные камни, которые замедлили интеграцию client-side предсказаний в проект:

1. У этого алгоритма есть ограничение, которое может оказаться довольно весомым: мы не можем прогнозировать дальше, чем на количество элементов в одном “сезоне”. То есть если, к примеру, мы прогнозируем продажи книг по месяцам год к году, то в таком случае мы не можем предсказывать дальше, чем на 12 месяцев.

2. Помимо пункта 1, у нас есть еще один лимит — у нас должно быть по меньшей мере 2 полных сезона с данными. Если взять тот же пример с книгами, то мы должны знать количество проданных книг в месяц за последние 24 месяца (2 года).

3. Иногда бывает так, что в рамках проекта мы предсказываем разные метрики, которые, очевидно, друг с другом не связаны. А это значит, что коэффиценты (альфа/гамма/бета) от одной метрики не подойдут к другой и нам надо вычислять их динамически. В этом случае мы вычисляем значение ошибки для разных показателей и в конце выбираем набор с наименьшей ошибкой (сниппет с примером такого вычисления будет как бонус в конце статьи). Очевидно, что это влияет на производительность, но в нашем случае это было незначительно.

4. Нам нужно такое количество записей, чтобы оно нацело делилось на размер сезона. Если сезон — это год, и в нем 12 записей (месяцев), то для прогноза нужно брать, например, 24/36/48 записей.

И еще одно: я не понял, в чем дело, но имея один набор исторических данных и разное количество записей, которые мы собираемся предсказать (например, есть история за 2 года, а предсказать хотим то на 3 месяца вперед, то на 12), мы получим разные прогнозы. Нам нужно было считать на 3 месяца вперед, поэтому я сделал еще один лайфхак — считал ошибку для обоих случаев и выбирал тот, в котором ошибка меньше.

Синяя линия — текущий гоод. Фиолетовая — предыдущий. Пунктир — прогноз.Прогнозирование по трем независимым метрикам (пунктирные линии). Синяя линия — текущий год.

Генерация признаков

Сгенерирую различные признаки с помощью ETNA и постараюсь объяснить, что они значат.

Лаги — это некоторое предыдущее значение временного ряда. Например, первый лаг — это вчерашнее значение. А пятый лаг — значение пять дней назад. Такие признаки необходимы для регрессионных моделей, например линейной регрессии или бустинга, чтобы получить информацию о прошлом ряда.

При прогнозировании модель смотрит на значения лагов и учится предсказывать значения самого временного ряда. Информацию о прошлом модель получает из лагов напрямуюКак проходит модель по таблице при обучении. Красным выделено то, что модель пытается спрогнозировать, а серым — обучающая выборка модели

Попробуем применить лаг с шагом 1 и посмотреть, что получится.Укажем список нужных нам лагов. В этом случае . Видим, что появилась новая колонка и в ней лежит наш лаг. Причем этот лаг мы сразу получили для всех сегментов благодаря тому, что ETNA способна работать с несколькими рядами одновременно.

Но что, если нам нужно сгенерировать несколько лагов? Это тоже легко сделать с помощью ETNA. Нужно указать в списке все лаги, которые нам нужны.

Можно использовать более сложные конструкции для задания лагов, например range или list comprehension

Статистики — еще один важный признак. Он хорошо себя показывает в регрессионных моделях, так как дает возможность передать моделям информацию о прошлом, но в отличном от лагов формате. Статистики бывают такие: среднее, медиана, среднеквадратичное отклонение, минимум или максимум на отрезке. 

Покажу, как этот признак работает на примере среднего. Запустить MeanTransform не сложнее, чем лаги.

Указали усреднение с окном 5Window — это сколько предыдущих значений мы хотим усреднить, чтобы получить значение в точке, — то самое окно. На первом шаге мы пытаемся усреднить пять значений, которые шли до первого значения включительно. Но до него данных не было, и поэтому заполняем самим числом 18. До значения 26 была только одна точка — 18. Поэтому усредняем 26 и 18. И так далее. Когда добираемся до числа, для которого есть все пять значений, усредняем их. И для всех следующих точек усредняем только пять значений — ведь именно такую ширину окна мы выбрали

С помощью такой фичи можно передавать модели информацию о среднем значении за последний месяц и неделю. А можно получать информацию о среднем значении за конкретные дни недели.

Усреднение двух точек, которые идут с шагом 2Расчет статистики с шагом 2

Даты — это временные метки, и их можно использовать. Например, для того, чтобы указывать дни недели, месяца, номер недели в месяце и в году или информацию о том, выходной сегодня или нет. 

Попробуем это сделать для нашего Dataset:

В DateFlagsTransform не нужно указывать, к какой колонке применить эту трансформацию, достаточно указать, какие именно данные мы хотим достать, как отдельные признаки. Я выбрал четыре признака, но в самом трансформе их девять, так что есть из чего выбрать

Праздники. C временными метками работает и HolidayTransform. Для работы он использует библиотеку holidays, в которой уже записаны основные праздники для большинства стран. Нам нужно указать только ISO-код страны, и готово:

Кажется, на Новый год в Финляндии отдыхают только 1 и 6 января =(

Логарифмирование. Я уже рассказал про трансформы, которые для генерации новых признаков используют сам ряд и которые используют его временную метку. Расскажу еще про один тип трансформов — те, что меняют сам ряд, или inplace-трансформы. Среди них самый простой — LogTransform. Он логарифмирует значения временного ряда.

Запускается LogTransform так же, как все предыдущие трансформы

Если мы хотим вернуть ряду его исходный вид, нужно воспользоваться методом inverse_transform:

Получается как в sklearn

Если мы хотим получить логарифмированные значения ряда, но не хотим «затирать» исходное, это можно сделать с помощью параметра .

Получили логарифмированное значение и сохранили исходное, чтобы оставить возможность считать и другие признаки от исходного значения

2) сезонное разложение (+ любая модель)

Если данные показывают некоторую сезонность (например, ежедневно, еженедельно, ежеквартально, ежегодно), может быть полезно разбить исходный временной ряд на сумму трех компонентов:

гдеS (T)является сезонной составляющей,Т (т)является компонентом цикла тренда, иR (T)является оставшимся компонентом.

Существует несколько методов для оценки такого разложения. Самый основной называетсяклассическое разложениеи состоит в:

1. Оценка тренда T (t) через скользящее среднее
2. ВычислительныйS (T)как средний ряд торгуемыхУ (т) -T (т)за каждый сезон (например, за каждый месяц)
3. Вычисление оставшейся серии какR (T) = Y (т) -T (т) -S (т)

Классическая декомпозициябыл расширеннесколькими способами. Его расширения позволяют:

• иметь непостоянную сезонность
• вычислить начальные и последние значения разложения
• избегать чрезмерного сглаживания

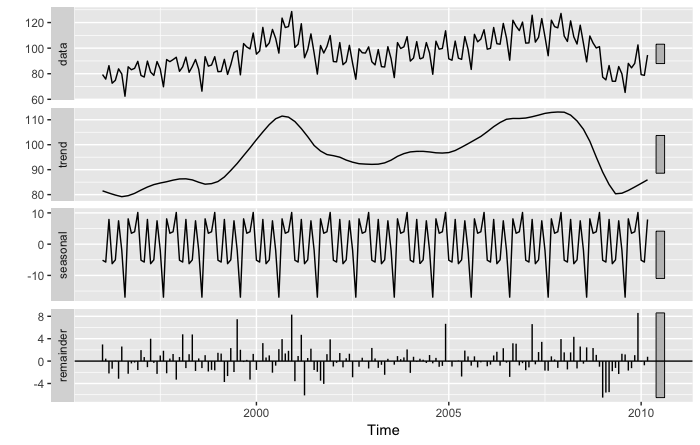Декомпозиция STL по данным индекса промышленного производства

Один из способовиспользовать разложение для прогнозированияЦели следующие:

1. Разложить обучающие временные ряды с помощью некоторого алгоритма декомпозиции (например, STL):Y (t) = S (t) + T (t) + R (t).
2. Вычислитьс учетом сезонных колебанийвременная последовательностьУ (т) -S (т), использованиелюбая модельВам нравится прогнозировать эволюцию сезонно скорректированных временных рядов.
3. Добавьте к прогнозам сезонность последнего периода времени во временном ряду (в нашем случаеS (T)за прошлый год).

На следующем рисунке показаны временные ряды индекса промышленного производства с учетом сезонных колебаний.

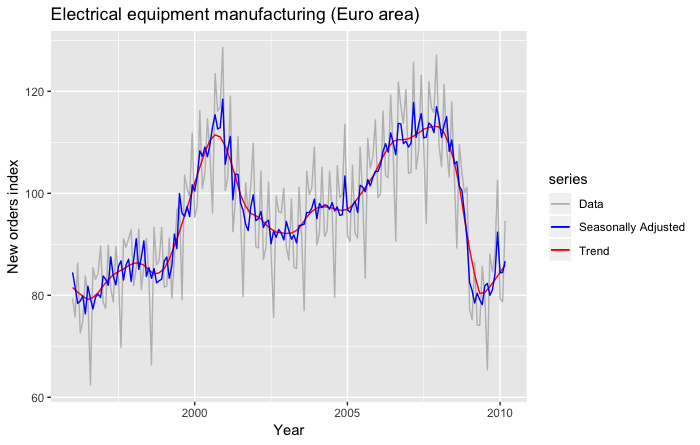
На следующем графике показаны прогнозы, полученные на 2007 год с использованием разложения STL и наивной модели для согласования с сезонно скорректированными временными рядами.

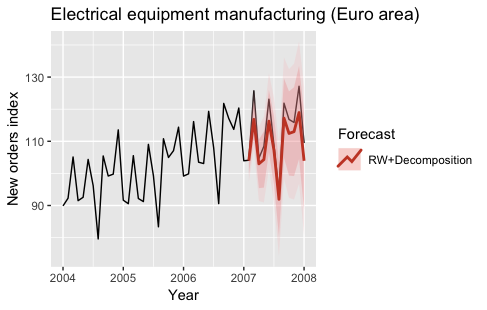
моделирование

Мы сосредоточимся исключительно на моделировании концентрации NOx. Поэтому мы удалим все остальные несоответствующие столбцы.

Затем мы импортируем Пророка.

Пророк требует, чтобы столбец даты был названД.С.и особенность столбца, который будет названYпоэтому мы вносим соответствующие изменения.

На данный момент наши данные выглядят так:

Затем мы определяем тренировочный набор. Для этого мы продержимся последние 30 записей для прогнозирования и проверки.

После этого мы просто инициализируем Prophet, подгоняем модель к данным и делаем прогнозы!

Вы должны увидеть следующее:

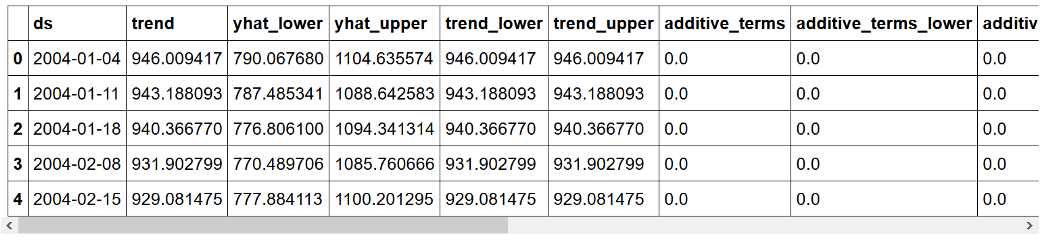
Вот,yhatпредставляет прогноз, в то время какyhat_lowerа такжеyhat_upperпредставляют нижнюю и верхнюю границу прогноза соответственно.

Пророк позволяет легко составить прогноз и мы получим:

Прогноз концентрации NOx

Как вы можете видеть, Пророк просто использовал прямую нисходящую линию, чтобы предсказать концентрацию NOx в будущем.

Затем мы проверяем, есть ли у временного ряда какие-либо интересные особенности, такие как сезонность:

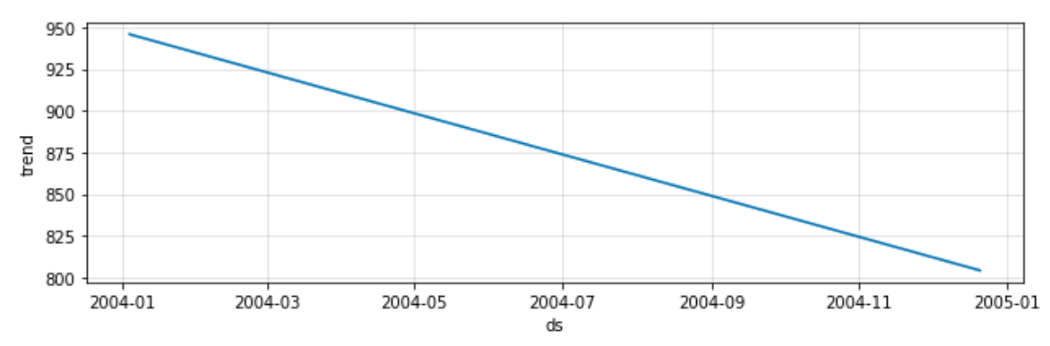
Здесь Пророк выявил только тенденцию к снижению без сезонности.

Оценивая производительность модели путем вычисления ее средней абсолютной процентной ошибки (MAPE) и средней абсолютной ошибки (MAE), мы видим, что MAPE составляет 13,86%, а MAE — 109,32, что не так уж и плохо! Помните, что мы не настроили модель вообще.

Наконец, мы просто строим прогноз с его верхней и нижней границами:

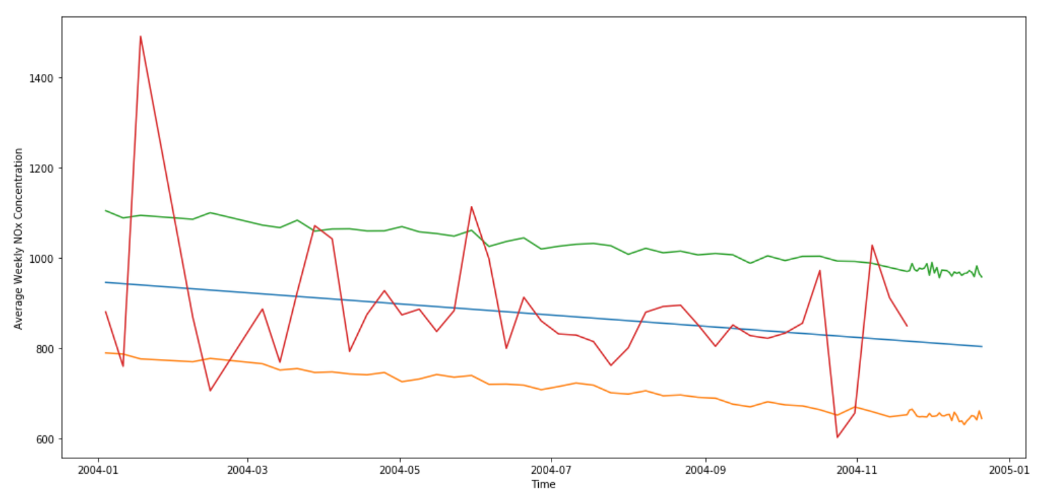Прогноз средней еженедельной концентрации NOx

Результаты прогнозирования

В узле ARIMAX три выходных порта:

• Выход модели
• Коэффициенты модели
• Сводка

После запуска обработчика ARIMAX можно открыть «Быстрый просмотр» на первом выходном порту и увидеть, что исходные данные дополнились следующими выходными столбцами:

• Продажи (руб.)ǀПрогноз. Прогноз объема продаж на основе предыдущих периодов.
• Продажи (руб.)ǀНижняя граница. Нижняя граница прогноза объема продаж на основе предыдущих периодов.
• Продажи (руб.)ǀВерхняя граница. Верхняя граница прогноза объема продаж на основе предыдущих периодов.
• Продажи (руб.)ǀОшибка аппроксимации. Среднее отклонение расчетных значений от фактических, будет отображаться, если установлена отметка в «Рассчитать ошибку аппроксимации».

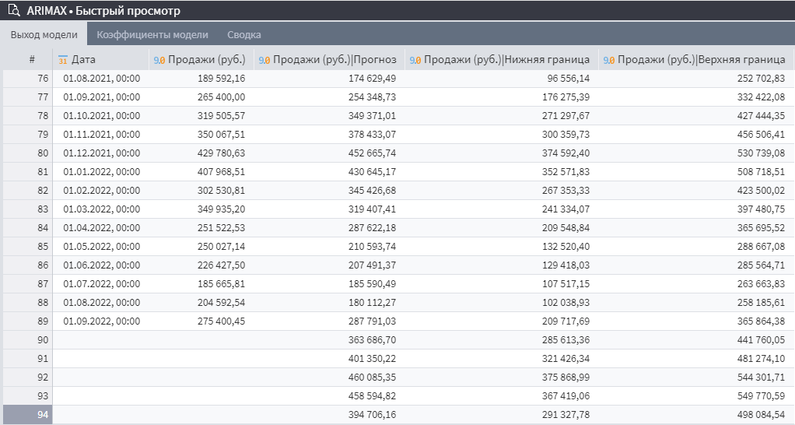
Выход модели ARIMAX

Причем прогнозные данные будут рассчитаны и для тех месяцев, по которым уже известен объем продаж, и для новых периодов. Стоит отметить, что в самом начале таблицы новые столбцы с прогнозами будут пустыми, их количество зависит от установленного значения в поле «Порядок AR части».

Если мы обратимся ко второму выходному порту, то увидим таблицу с коэффициентами модели, а к третьему — сводку значений переменных, показывающих количество примеров, ошибки на обучающем множестве, информационные критерии, коэффициенты детерминации, числа степеней свободы.

Данные выходных портов дают исчерпывающую информацию о выполненном прогнозе, но табличное представление сложно воспринимать, поэтому в большинстве случаев потребуются визуализаторы.

Прежде, чем переходить к построению графиков, необходимо заполнить значения временного ряда для появившихся строк, иначе график прогноза будет отображаться только на исходном временном периоде, а значения на горизонте прогноза не будут отражены. Для этого добавим узел «Калькулятор».

В настройках узла создадим переменную AllDates, которая будет содержать все значения временного ряда. Расчет будет строиться с помощью функции условия If. Если поле даты пустое, то функция AddMonth добавляет необходимое количество месяцев к последнему известному значению, в противном случае вносит ту дату, которая указана в поле.

Для того, чтобы вычислить количество месяцев, необходимо сначала найти разность между номером текущей строки (функция RowNum()) и количеством уникальных значений поля Date (функция Stat(«Date», «UniqueCount»)), а затем добавить к полученному результату 2

Важно учитывать, что нумерация строк начинается с 0, а в количестве уникальных значений присутствуют не только исходные даты, но и пустое значение в появившихся после прогноза строках, именно поэтому вводится цифра 2

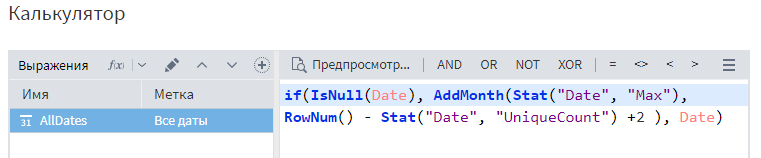
Калькулятор Loginom

После выполнения узла «Калькулятор» в таблице на его выходном порту появится столбец «Все даты».

Теория временных рядов

Мы тут не за теорией, но некоторые основные понятия ввести тем не менее надо. За более глубоким разъяснением советую обратиться к учебникам Светуньковых (у них, кстати, есть сайт c блогом).

Итак, под временным рядом понимаются последовательно измеренные через некоторые (зачастую равные) промежутки времени данные. Например, люди на протяжении ста лет измерядли тепрературу воздуха в каком-то мести и получили временной ряд. Самое ценное, что можно делать с временными рядами — это прогнозировать их дальнейшние значения. Прогноз — это всегда вероятностное, но научно обоснованное суждение о созможных будущих состояниях объекта или явления, в нём всегда есть доля ошибки. В лучшем случае эта ошибка случайная, в худшем — систематическая (о видах ошибок читайте в лекции «честные модели»). Чтобы построить прогноз необходима математическая модель, которая задаст правило для его расчёта, причём эта модель будет стохастической, поскольку в ней обязательно присутствует неопределённость в виде ошибки.

Помимо этого на временных рядах можно тестировать различные гипотезы: есть ли между двумя временными рядами связь, являются ли они стационарными или нет. Стационарность — это свойство процесса не менять свои характеристики со временем, т.е. если во временном ряду есть какой-либо тренд, он уже не стационарен. Это неудобно, поскольку многие модели и тесты предполагают стационарность временных рядов, а на нестационарных рядах их результаты ненадёжны.

Модели временных рядов

Прежде чем перейти к сложным моделям временных рядов, мы обсудим некоторые простые модели, которые составляют основу для дальнейших предсказаний. Если сложный метод не дает лучших результатов, то нет смысла их использовать.

1. Среднее значение — прогнозы равны среднему значению временного ряда.
2. Наивный — прогнозы равны последнему значению временного ряда.
3. Сезонный наивный — прогнозы на данный сезон равны значению этого сезона за полный период до, например, Прогнозы на январь 2019 года равны значению временных рядов на январь 2018 года.

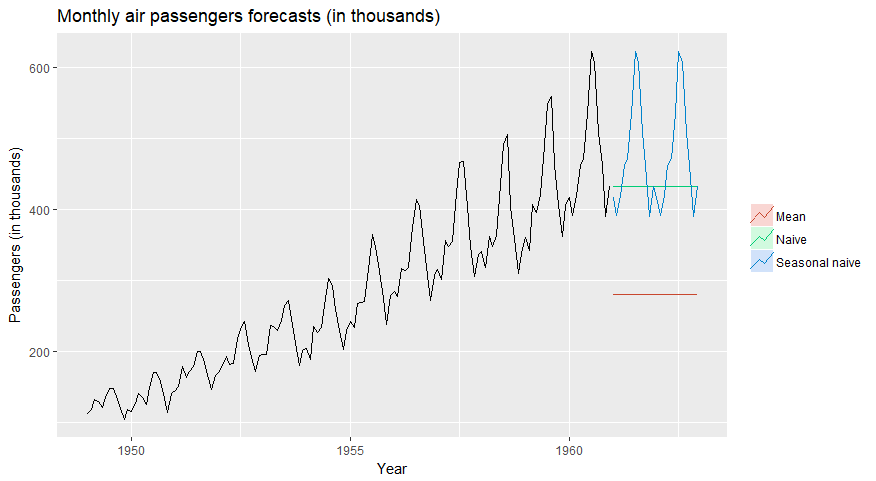
Рис. Базовые прогнозы месячных пассажиров авиакомпании.

Линейная модель временного ряда (TSLM) — это просто модель линейной регрессии, которая прогнозирует требуемое значение на основе некоторых предикторов, чаще всего линейного тренда и сезонности:

гдеXI, тнекоторые предикторы,искусственный интеллекта такжебявляются коэффициентами регрессии для оценки. Два наиболее часто используемых предиктора — это тренд и сезонность. Первый просто моделирует линейный тренд в данных — модель с единственным предиктором тренда может быть записана как:

Предсказатели сезонности — это фиктивные переменные, указывающие период (например, месяц, квартал), для которого сделаны прогнозы.

где a (0,1) — параметр сглаживания, который следует оценить. Метод, представленный выше, может быть расширен за счет включения тренда (метод Холта или двойного экспоненциального сглаживания) или тренда и сезонности (метод Холта-Уинтерса, называемый тройным экспоненциальным сглаживанием). В этих моделях коэффициенты тренда и сезонности также вычисляются как средневзвешенное значение некоторых выражений. Хотя идея довольно проста, формулы более сложны, и мы не будем вдаваться в технические детали. Заинтересованный читатель может обратиться к книге Хиндмана и Афанасопулоса о прогнозировании временных рядов .

тогда как скользящее среднее (Массачусетс) моделирует влияние шума на будущие значения.

гдеи дрявляются случайными условиями шума. В приведенном выше примере каждый шумовой член влияет на три последовательныхугзначения. В действительности такие термины шума могут отражать некоторые неожиданные события, например, заявления политиков, влияющие на фондовые рынки.

В действительности такие термины шума могут отражать некоторые неожиданные события, например, заявления политиков, влияющие на фондовые рынки.

Модели AR и MA могут быть объединены в модель ARMA простым способом, как показано ниже:

интегрированныйчасть ARIMA соответствует техническому вопросу о том, как устанавливаются модели ARMA. По сути, имеет смысл только подгонять их к стационарным временным рядам. Один из способов стационарного размещения нестационарных данных состоит в том, чтобы вычесть из них их запаздывающие значения (различие их). Это то, что делает ARIMA перед установкой ARMA — она ​​несколько раз различает данные, пока не получит достаточно стационарные данные.

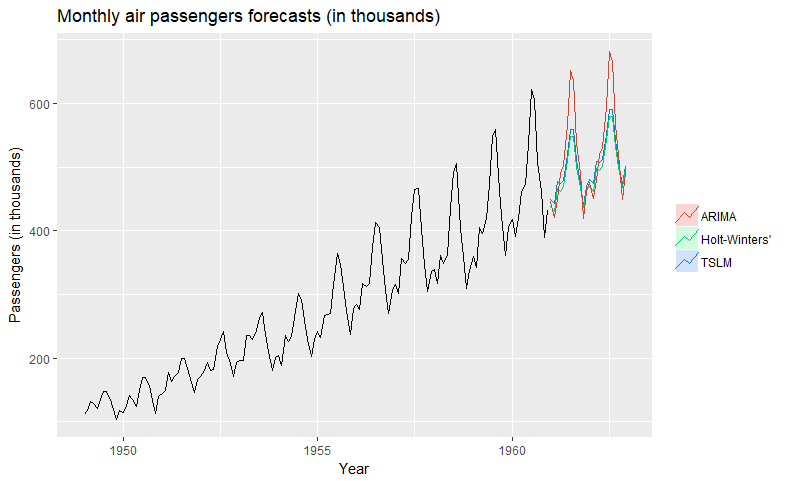
Рис. Прогнозы месячных пассажиров авиакомпаний.

Шаг 2

Так как мы рассматриваем аддитивную модель вида: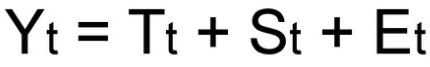 

Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.

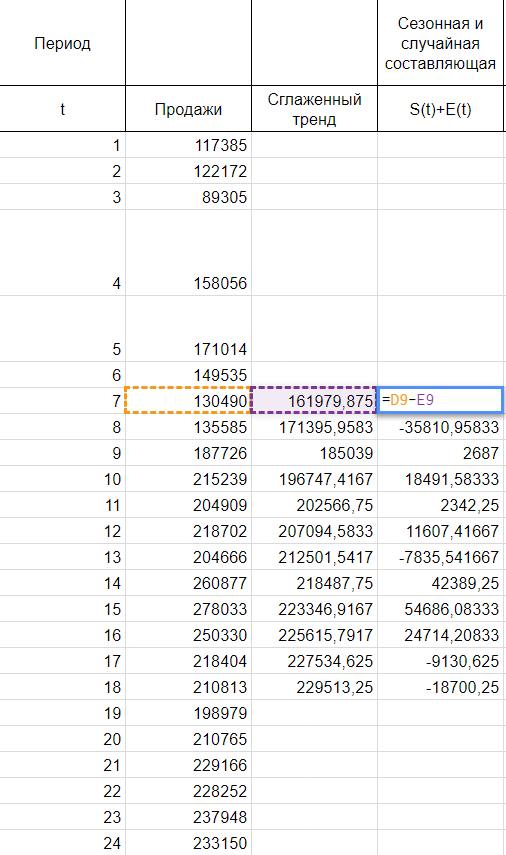
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.

Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:

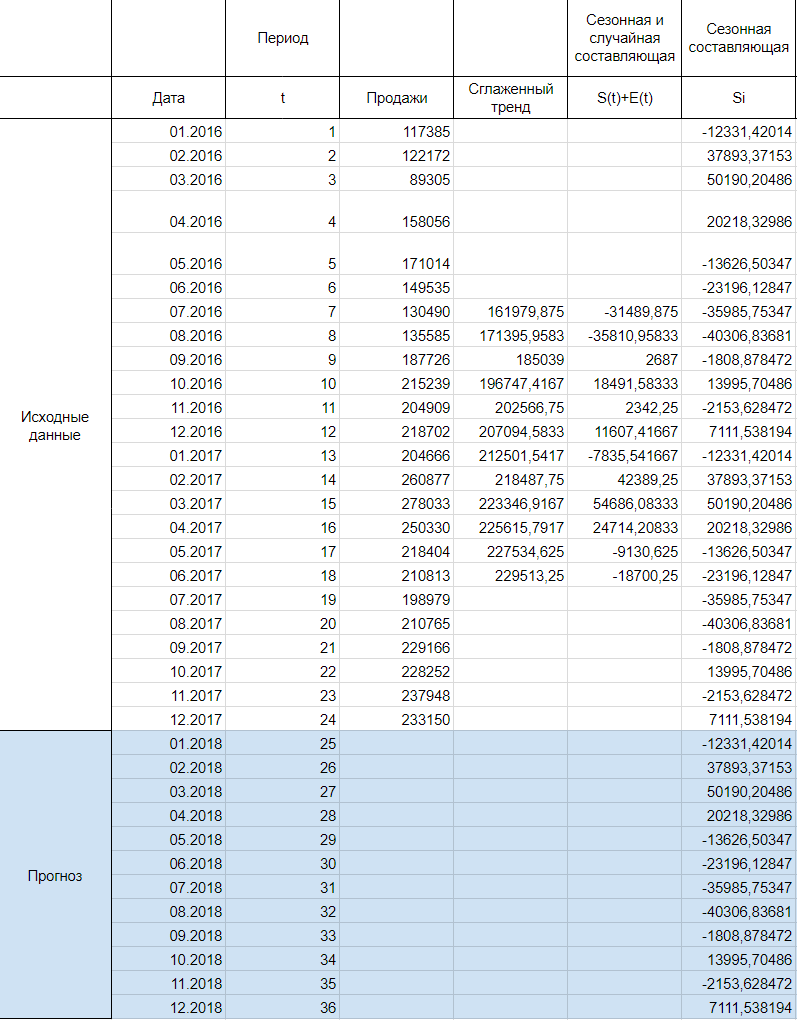
В чем суть?

На своей работе в качестве React Front-end разработчика я обычно работаю с дашбордами и различными видами данных. В какой-то момент нам понадобилось добавить предсказания по метрикам, а в команде не было специалистов по анализу данных, которые могли бы этим заняться.

Проблема 1

Очень большой объем данных для предсказания и малое количество записей — тысячи возможных срезов данных, но малое количество исторических данных.

Проблема 2

Очень большая нагрузка на ребят из бэкенда, так что они физически не могли справиться с этой задачей. Ограниченная квота Java инстансов в компании на проект. Все эксперты заняты, согласовывать долго, делать долго, ждать бекенд долго.

Модель скользящего среднего, Moving Average (MA)

Согласно модели скользящего среднего актуальное значение целевой переменной складывается с средней величины и суммы случайных ошибок за прошлые периоды с некоторыми их весами.

В общем виде формула модели скользящей средней порядка qqq (то есть учитывающая qqq временных периодов) выглядит как сумма произведений значений за предыдущие периоды на веса этих значений:

MAq=μ+∑<em>j=qθ<em>j⋅ϵt−j,MA_{q}=\mu+\sum <em>{j=0}^{q}\theta</em>{j}\cdot \epsilon_{t-j},MAq​=μ+∑<em>j=qθ<em>j⋅ϵt−j​,
где ϵ\epsilonϵ — это ошибка, белый шум, θ\thetaθ — вес шума за определённый период модели (θ\theta_{0}θ​ можно считать равным 111 без ограничения общности).

Таким образом, модель скользящего среднего значения по сути представляет собой линейную регрессию, где актуальное значение временного ряда зависит от величины белого шума в текущем периоде ttt и qqq предыдущих.

Рассмотрим подробнее модель первого порядка, которая будет выглядить следующим образом:

MA1=μ+ϵt1+θϵt−1.MA_1=\mu+\epsilon_t1+\theta\epsilon_{t-1}.MA1​=μ+ϵt​1+θϵt−1​.

Если параметр θ\thetaθ равен нулю, мы получаем обычный белый шум — модель скользящей средней нулевого порядка MA(0).

Если параметр θ\thetaθ меньше 0, то мы можем говорить о тенденции временного ряда возвращаться к среднему уровню (Mean Reversion), поскольку ошибка за текущий период будет компенсироваться ошибкой за прошлый период. Если же параметр θ\thetaθ больше 0, мы можем говорить о моментум.

Конструируем SQL-запрос

Для начала сгенерируем немного случайных данных за предыдущие пару лет:

Да, это даст нам не вполне корректные значения результата прогнозирования, но поможет отладить алгоритм, который вы сможете повторить уже на более реальных данных.

«Си, бейсик, паскаль… русский со словарем»

Поскольку алгоритм у нас итеративный, то на SQL для этого мы будем использовать рекурсивный запрос. В теории, можно было бы вывести некую мегасложную , но мы будем действовать проще.

Согласно приведенной выше формуле, нам понадобятся суммы за d последовательных дней периода до конкретной даты и значение в этой дате. Поэтому сначала Преобразуем интервалы в количество дней:

Чтобы не извлекать повторно эти данные каждый раз из таблицы и пересчитывать заново, сложим их в json-словарь в формате :

Возьмем типичный шаблон для итеративной работы со словарем, аналогичный рассмотренному в статье SQL HowTo: пишем while-цикл прямо в запросе, или «Элементарная трехходовка»:

То все присказка была… Пора реализовать сам алгоритм вычисления следующего значения. Сначала потренируемся вычислять значение дня для первого шага, без рекурсии, а для этого продолжим вывод значения с использованием уже агрегированных данных:

A = A’ — = sum — sum

Тут мы заменили сумму на интервале в день как разность сумм на -интервале и единичном. К счастью, мы ранее позаботились, чтобы они у нас были, и теперь наш модельный запрос выглядит так:

Обратите внимание, что сначала мы вычислили по всему набору периодов ожидаемое значение , и только потом через использовали его для пересчета сумм по каждому периоду. Теперь осталось собрать все в один запрос:

Теперь осталось собрать все в один запрос:

Пользуйтесь на свой страх и риск.

Автоматическое машинное обучение (AutoML)

Современная Data Science стала весьма востребованной частью IT сферы. Специалисты собирают данные, занимаются их очисткой, пробуют различные модели, производят валидацию, выбирают лучшие из них. И все это для того, чтобы предоставить бизнесу решение, которое принесет наибольшую пользу. При этом, некоторые этапы получения таких решений с каждым годом все больше и больше автоматизируются. Как правило, это касается наиболее рутинных частей. Таким образом освобождается время экспертов для более важных задач.

Итак, представим, что перед специалистом стоит задача построить модель машинного обучения и “обернуть” её в web-сервис, чтобы эта самая модель выполняла полезную работу — предсказывала что-либо. Но прежде чем дойти до этапа обучения модели, требуется пройти несколько шагов, в том числе:

• собрать данные из множества источников, очистить их;
• осуществить предобработку, нормализацию, закодировать некоторые из признаков;
• отобрать наиболее полезные из них, либо синтезировать на их основе новые;
• удалить возможные выбросы в данных.

Такие многоступенчатые последовательности операций, включающие этапы от первичной обработки данных до обучения модели и составления прогнозов, называют пайплайнами. Работать с пайплайнами уже несколько сложнее, чем с одиночными моделями машинного обучения, так как чем больше составных блоков, тем больше гиперпараметров, которые нужно оптимизировать. Также выше вероятность того, что на каком-нибудь этапе возникнет ошибка, да и в целом такую более громоздкую систему труднее настраивать и контролировать ее поведение. Для решения этой проблемы реализованы специальные инструменты — MLFlow, Apache AirFlow и т. д — что-то вроде workflow management system (WMS) в мире машинного обучения. Они призваны упростить контроль за состоянием пайплайнов обработки данных.

Почему потребность в таких инструментах возникла, ведь раньше обходились без них?

Более амбициозной задачей в данной области машинного обучения является автоматическая генерация этих пайплайнов. Существует несколько фреймворков, которые предоставляют подобные функции, среди open-source, например это TPOT, AutoGluon, MLJAR или H2O. Такие AutoML фреймворки решают задачу оптимизации вида “построить такой пайплайн, который дает конечный прогноз с наименьшей (среди всех рассмотренных решений) ошибкой”. В основном структура пайплайна зафиксирована и подбираются только гиперпараметры, но некоторые фреймворки способны получать в качестве решения модели произвольной структуры. Данная оптимизационная задача (нахождения пайплайна произвольной структуры) решается как правило при помощи эволюционных алгоритмов, примеры: фреймворки TPOT и FEDOT.

Существуют также и проприетарные SaaS-решения, такие как DataRobot, GoogleAutoTables, Amazon SageMaker, которые помогают не только автоматизировать ML эксперименты, но и предоставляют возможности AutoML.

Как правило, AutoML библиотеки и сервисы успешно решают две самые популярные задачи в машинном обучении: классификация и регрессия на табличных данных. Реже поддерживаются задачи, связанные с обработкой изображений, текста и прогнозирования временных рядов. В рамках данной статьи мы не будем рассматривать плюсы и минусы известных решений, а остановимся на возможностях автоматического машинного обучения в задаче прогнозирования временных рядов.

Вместо итогов

В статье мы рассмотрели различные особенности данных, которые могут существенно влиять на качество прогнозирования. В их числе могут выступать аномальное поведение, выбросы, сезонность, тренд и многое другое. Обнаруживать эти особенности нам помогают методы EDA, при этом большую часть интересных находок из этих методов можно легко добавить в пайплайн прогнозирования и задешево улучшить качество нашей модели. Надеюсь, мне удалось убедить вас, что EDA — это полезный шаг при построении пайплайна.

Если статья вам понравилась, не стесняйтесь ставить нам звездочки на GitHub. Для тех, кто хочет самостоятельно покопаться в данных и попробовать все наши методы EDA в деле, прилагаю код для загрузки данных.