Что называется числовой последовательностью

Использование последовательностей в Adobe Premiere Pro

Как только вы научитесь использовать последовательности, они могут стать очень мощным инструментом для вашего рабочего процесса, когда у вас есть длительные и трудные проекты. Он обеспечивает отличный метод организации и помогает вам все делать прямо, без необходимости создавать дополнительные проекты Premiere.

Надеюсь, это руководство помогло вам понять, как работают последовательности в Premiere, и вы сможете начать использовать их в своих собственных редактирование проектов.

Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)

Основные свойства бесконечно малых последовательностей

Теорема:

Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности.

Доказательство:

Пусть — бесконечно малые последовательности. Требуется доказать, что последовательность бесконечно малая. Пусть — произвольное положительное число, — номер, начиная с которого —номер, начиная с которого (Такие номера найдутся по определению бесконечно малой последовательности.) Возьмем тогда при n>N будут одновременно выполняться два неравенства: Следовательно, при n>NЭто значит, что последовательность бесконечно малая.

Следствие:

Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема:

Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство:

Пусть — бесконечно малые последовательности. Требуется доказать, что последовательность бесконечно малая. Так как последовательность бесконечно малая, то для любого существует номер , такой, что а так как также бесконечно малая последовательность, то для существует номер такой, что при Возьмем тогда при n>N будут выполняться оба неравенства. Следовательно, при п> N

Это означает, что последовательность бесконечно малая.

Следствие:

Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Замечание:

Частное двух бесконечно малых последовательностей может не быть бесконечно малой последовательностью и может даже не иметь смысла. Например, если то все элементы равны единице и данная последовательность является ограниченной. Если то последовательность бесконечно большая, а если то — бесконечно малая. Если, начиная с некоторого номера, элементы равны нулю, то не имеет смысла.

Теорема:

Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

Доказательство:

Пусть — ограниченная, а — бесконечно малая последовательности. Требуется доказать, что последовательность бесконечно малая. Так как последовательность ограничена, то существует число А>0 такое, что любой элемент удовлетворяет неравенству Возьмем любое . Поскольку последовательность бесконечно малая, для положительного числа существует номер N такой, что при n>N выполняется неравенство Следовательно, при n>N:

Это означает, что последовательность бесконечно малая.

Следствие:

Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Перейдем теперь к одному из важнейших в математическом анализе понятию предела числовой последовательности.

Классификация от последовательности к последовательности Используя глубокое обучение

Скрипт Open Live Script

В этом примере показано, как классифицировать каждый временной шаг данных о последовательности с помощью сети долгой краткосрочной памяти (LSTM).

Чтобы обучить глубокую нейронную сеть классифицировать каждый временной шаг данных о последовательности, можно использовать сеть LSTM от последовательности к последовательности. Сеть LSTM от последовательности к последовательности позволяет вам сделать различные прогнозы для каждого отдельного временного шага данных о последовательности.

Этот пример использует данные о датчике, полученные из смартфона, который изнашивают на теле. Пример обучает сеть LSTM, чтобы распознать действие владельца, данного данные временных рядов, представляющие показания акселерометра в трех различных направлениях. Обучающие данные содержат данные временных рядов для семи человек. Каждая последовательность имеет три функции и варьируется по длине. Набор данных содержит шесть учебных наблюдений и одно тестовое наблюдение.

Загрузите данные о последовательности

Загрузите данные о распознавании деятельности человека. Данные содержат семь временных рядов данных о датчике, полученных из смартфона, который изнашивают на теле. Каждая последовательность имеет три функции и варьируется по длине. Три функции соответствуют показаниям акселерометра в трех различных направлениях.

load HumanActivityTrain
XTrain

XTrain=6×1 cell
    {3×64480 double}
    {3×53696 double}
    {3×56416 double}
    {3×50688 double}
    {3×51888 double}
    {3×54256 double}

Визуализируйте одну обучающую последовательность в графике. Постройте первую функцию первой обучающей последовательности и окрасьте график согласно соответствующему действию.

X = XTrain{1}(1,:);
classes = categories(YTrain{1});

figure
for j = 1:numel(classes)
    label = classes(j);
    idx = find(YTrain{1} == label);
    hold on
    plot(idx,X(idx))
end
hold off

xlabel("Time Step")
ylabel("Acceleration")
title("Training Sequence 1, Feature 1")
legend(classes,'Location','northwest')

Задайте сетевую архитектуру LSTM

Задайте архитектуру сети LSTM. Задайте вход, чтобы быть последовательностями размера 3 (количество функций входных данных). Задайте слой LSTM с 200 скрытыми модулями и выведите полную последовательность. Наконец, задайте пять классов включением полносвязного слоя размера 5, сопровождаемый softmax слоем и слоем классификации.

numFeatures = 3;
numHiddenUnits = 200;
numClasses = 5;

layers = ;

Задайте опции обучения. Установите решатель на . Обучайтесь в течение 60 эпох. Чтобы препятствовать тому, чтобы градиенты взорвались, установите порог градиента к 2.

options = trainingOptions('adam', ...
    'MaxEpochs',60, ...
    'GradientThreshold',2, ...
    'Verbose',0, ...
    'Plots','training-progress');

Обучите сеть LSTM с заданными опциями обучения с помощью . Каждый мини-пакет содержит целый набор обучающих данных, таким образом, график обновляется однажды в эпоху. Последовательности очень длинны, таким образом, это может занять время, чтобы обработать каждый мини-пакет и обновить график.

net = trainNetwork(XTrain,YTrain,layers,options);

Протестируйте сеть LSTM

Загрузите тестовые данные и классифицируйте действие на каждом временном шаге.

Загрузите тестовые данные деятельности человека. содержит одну последовательность размерности 3. содержит последовательность категориальных меток, соответствующих действию на каждом временном шаге.

load HumanActivityTest
figure
plot(XTest{1}')
xlabel("Time Step")
legend("Feature " + (1:numFeatures))
title("Test Data")

Классифицируйте тестовые данные с помощью .

YPred = classify(net,XTest{1});

В качестве альтернативы можно сделать прогнозы одним временным шагом за один раз при помощи . Это полезно, когда у вас есть значения временных шагов, прибывающих в поток. Обычно, это быстрее, чтобы сделать прогнозы на полных последовательностях когда по сравнению с созданием прогнозов один временной шаг за один раз. Для примера, показывающего, как предсказать будущие временные шаги путем обновления сети между одним прогнозами временного шага, смотрите, что Временные ряды Предсказывают Используя Глубокое обучение.

Вычислите точность прогнозов.

acc = sum(YPred == YTest{1})./numel(YTest{1})

acc = 0.9998

Сравните прогнозы с тестовыми данными при помощи графика.

figure
plot(YPred,'.-')
hold on
plot(YTest{1})
hold off

xlabel("Time Step")
ylabel("Activity")
title("Predicted Activities")
legend()

Как редактировать и удалять последовательности

Если вы используете последовательности, также важно знать все тонкости их редактирования. Например, вы можете изменить некоторые настройки или удалить ненужную последовательность

Редактирование последовательностей

Чтобы отредактировать аспекты ваших последовательностей, перейдите на верхнюю панель в Premiere и выберите Sequence. Вы увидите раскрывающийся список вариантов, которые вы можете изменить в своей последовательности.

Вверху вы можете выбрать настройки последовательности, чтобы напрямую изменить их. Это изменит только настройки выбранной вами последовательности, поэтому убедитесь, что вы выбрали правильный, прежде чем переходить к настройкам и изменять их.

Подпоследовательности

Вы также можете создавать так называемые подпоследовательности, которые действуют очень аналогично вложенным последовательностям. Они никоим образом не изменят клипы на вашей фактической шкале времени, а вместо этого будут созданы отдельно на панели «Проект». Сделать это:

1. Найдите на временной шкале клип, который вы хотите превратить в подпоследовательность.

1. Щелкните его правой кнопкой мыши и выберите «Создать подпоследовательность».

1. Подпоследовательность появится на панели «Проект».

Вложенный эпизод возьмет все клипы из вашего эпизода и превратит его в гнездо. Вам просто нужно дважды щелкнуть гнездо, чтобы редактировать свои клипы очередной раз.

Удаление последовательности

Если вы решите, что вам больше не нужны эпизоды на шкале времени, их очень легко удалить.

Выберите все клипы в последовательности и нажмите Backspace, чтобы удалить их.

Вверху шкалы времени найдите заголовок эпизода и щелкните маленький крестик рядом с ним. Это должно убрать последовательность из поля зрения.

Если вы вложили последовательность в другое место, вы все равно можете дважды щелкнуть по ней, чтобы снова открыть ее на шкале времени.

Чтобы удалить вложенную последовательность, просто выберите ее на шкале времени и нажмите Backspace.

Числовые последовательности

Числовые последовательности и арифметические действия над ними. Числовые последовательности изучают уже в средней школе. Примерами таких последовательностей могут служить: 1) последовательность всех членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных л-угольников, вписанных в данную окружность; 3) последовательность приближенных значений

Уточним и расширим понятие числовой последовательности.

Определение:

Если каждому числу п из натурального ряда чисел поставлено в соответствие вещественное число то множество вещественных чисел

называется числовой последовательностью или просто последовательностью*

Числа будем называть элементами (или членами) последовательности (1), символ — общим элементом (или членом) последовательности, а число п — его номером. Сокращенно последовательность (1) будем обозначать символом

Так, например, символ обозначает последовательность Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула *Другими словами, числовую последовательность можно определить как множество пар чисел, в которых первое число принимает последовательно значения 1, 2, 3, … задает последовательность: 0,2, 0,2, … Обращая дробь в десятичную и оставляя один, два, три и т. д. знака после запятой, получаем последовательность

По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами.

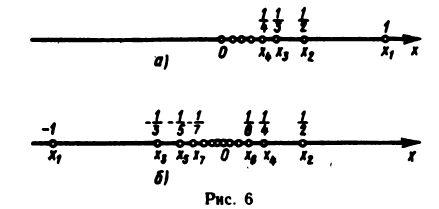
Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. На рис. 6, а

и б изображены соответственно последовательности и

Введем арифметические действия над числовыми последовательностями. Пусть даны последовательности

Произведением последовательности на число m назовем последовательность суммой данных последовательностей назовем последовательность

разностью — последовательность произведением — последовательность частным — последовательность если все члены последовательности отличны от нуля.

Указанные действия над последовательностями символически записываются так: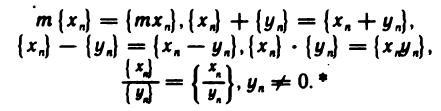

Понятие последовательности

Посмотрим на несколько рядов чисел и порассуждаем.

По какому принципу составлен ряд чисел 1, 2, 3, 4, 5 и т.д.? Всё просто: к каждому новому числу прибавляют единицу. 

А какой принцип в ряде чисел 2, 4, 6, 8 и т.д.? Здесь к каждому новому числу прибавляют 2. 

Что можно сказать про ряд 2, 4, 8, 16, 32 и т.д.? Каждое новое число умножают на 2. 

Все приведенные выше ряды чисел будут называться последовательностью. Как описать ее одним термином?

Ненадолго вспомним функции чисел. Разберем функцию f(x)=x+1. Если x = 0, то f(x) = 1.Если x = 1, то f(x) = 2.Если x = 2, то f(x) = 3.Если x = 3, то f(x) = 4.

Внимательно посмотрим на значения функции: это и будет наша первая последовательность 1, 2, 3, 4, 5. Мы можем сделать вывод, что последовательность можно задать с помощью функции. 

На самом деле, любая последовательность и есть функция. Теперь дадим определение. 

Последовательность — функция, заданная на множестве натуральных чисел или его части. 

То есть подставлять в такую функцию можно только натуральные числа. 

Подробнее про функцию, ее значение, область определения и другие свойства можно прочесть в статье «Определение и график функции». 

Аргумент будет обозначать порядковый номер числа в последовательности. Первое число в последовательности будет задаваться х = 1, второе число х = 2, n число как х = n. 

Числа, которые образуют последовательность, — это члены последовательности. И у каждого члена последовательности есть свой порядковый номер. 

Как же обозначаются члены последовательности? Не будем же мы каждый раз писать “двадцатый член последовательности” или что-то подобное? 

Для членов последовательности существует свое обозначение: an, где индекс после буквы а обозначает порядковый номер члена последовательности. 

Например, 

• а₁ — первый член последовательности, 
• а₂₀ — двадцатый член последовательности, 
• а₁₀₀ — сотый член последовательности и так далее. 

Таким образом можно обозначить любой член последовательности. 

Как мы привыкаем к последовательностям на протяжение нашей жизни?Вспомним считалочки, которые мы использовали в играх в детстве: “Раз, два, три, четыре, пять, вышел зайчик погулять”.  Первая строчка многих подобных считалочек — это последовательность натуральных чисел 1, 2, 3, 4, 5.Дальше в школе на уроках физкультуры нас распределяют по командам, присваивая каждому свой номер. И это тоже последовательность.Потом мы поступаем в вуз и попадаем в списки абитуриентов, тоже — в ещё одну последовательность.

Диаграммы Вороного

площади

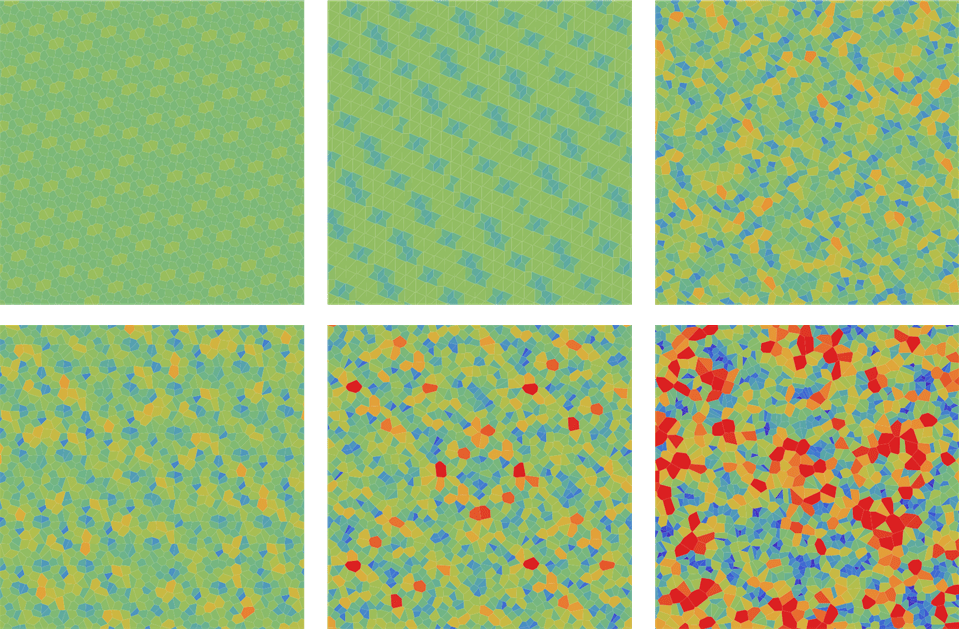Рисунок 4. Визуализация формы диаграмм Вороного на основании площади каждого многоугольника Вороного для (i) -последовательности; (ii) (2,3)-последовательности на основе простых чисел; (iii) (2,3)-последовательности Холтона, (iv) Нидеррайтера; (v) Соболя; и (iv) простое случайное сэмплирование. Цвета обозначают количество сторон каждого многоугольника Вороного. Повторюсь: очевидно, что -последовательность обеспечивает гораздо более равномерное распределение, чем любые другие последовательности с низким расхождением.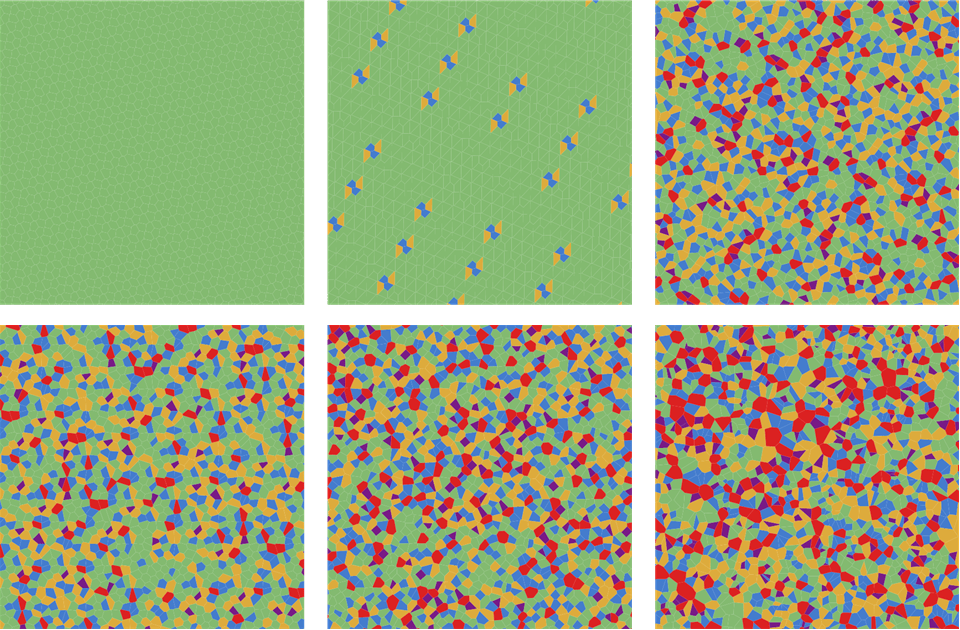Рисунок 5. Визуализация формы диаграмм Вороного на основании числа сторон каждого многоугольника Вороного для (i) -последовательности; (ii) (2,3)-последовательности на основании простых чисел; (iii) (2,3)-последовательности Холтона, (iv) Нидеррайтера; (v) Соболя; и (iv) простого случайного сэмплирования. Цвета обозначают количество сторон каждого многоугольника Вороного. Повторюсь: очевидно, что -последовательность обеспечивает гораздо более равномерное распределение, чем любые другие последовательности с низким расхождением.

Получение вложенных параметров

и похожи на соответствующие функции, доступные для списков, за исключением того, что фильтрация и выбор не выполняются до оценки элементов последовательности.

создает последовательность из другой последовательности, но ограничивает последовательность указанным количеством элементов. создает новую последовательность, содержащую только указанное количество элементов с начала последовательности. Если в последовательности меньше элементов, чем указано, вызывает исключение . Разница между и заключается в том, что не приводит к ошибке, если число элементов меньше указанного числа.

В следующем коде показано поведение и различия между и .

Выходные данные до возникновения ошибки приведены ниже.

С помощью можно указать функцию предиката (логическую функцию) и создать последовательность из другой последовательности, состоящей из этих элементов исходной последовательности, для которой является предикат , но остановиться перед первым элементом, для которого возвращается предикат. возвращает последовательность, которая пропускает указанное число первых элементов другой последовательности и возвращает остальные элементы. возвращает последовательность, которая пропускает первые элементы другой последовательности до тех пор, пока возвращается предикат, а затем возвращает оставшиеся элементы, начиная с первого элемента, для которого возвращается предикат.

В следующем примере кода показано поведение и различия между , и .

Выходные данные выглядят следующим образом.

Ограниченность сходящейся последовательности.

Последовательность \(\left\{x_n\right\}\) называется ограниченной снизу, если существует такое число С₁, что все члены последовательности удовлетворяют условию \(x_n\geq C_1\), то есть

$$ \exists \ C_1: \ \forall n \ \in\mathbb{N} \ \rightarrow x_n\geq C_1\nonumber $$

Последовательность \(\left\{x_n\right\}\) называется ограниченной сверху, если

$$ \exists \ C_2: \ \forall n \ \in\mathbb{N} \ \rightarrow x_n\leq C_2\nonumber $$

Последовательность, ограниченная как сверху, так и снизу, называется ограниченной, то есть последовательность \(\left\{x_n\right\}\) называется ограниченной, если

$$ \exists \ C_1 \ \exists \ C_2: \ \forall n \ \in\mathbb{N} \ \rightarrow C_1\leq x_n\leq C_2\label{ref5} $$

Заметим, что условие \eqref{ref5} равносильно следующему

$$ \exists \ C > 0: \ \forall n\in\mathbb{N}\rightarrow\left|x_n\right|\leq C\label{ref6} $$

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Теорема 2.

Если последовательность имеет предел, то она ограничена.

Пусть последовательность \(\left\{x_n\right\}\) имеет предел равный \(a\). По определению предела для \(\varepsilon=1\) найдем такой номер N, что при всех \(n\geq N\) имеет место неравенство \(\left|x_n-a\right|<1\). Так как модуль суммы не превосходит суммы модулей, то
$$ \left|x_n\right|=\left|x_n-a+a\right|\leq\left|x_n-a\right|+\left|a\right|\nonumber$$

Поэтому при всех \(n > N\) выполняется $$\left|x_n\right|<1+\left|a\right|\nonumber$$

Положим \(c=max(1+\left|a\right|, \ \left|x_1\right|,\ldots,\left|x_{N-1}\right|)\), тогда \(\left|x_n\right|\leq C\) при всех \(n\in\mathbb{N}\), то есть последовательность \(\left\{x_n\right\}\) ограничена.

Замечание 1.

В силу всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся. Например, последовательность \(\left\{\left(-1\right)^n\right\}\) ограничена, но не является сходящейся.

Замечание 2.

Если условие \eqref{ref6} не выполняется, то есть $$ \forall C > 0\quad\exists n_C\in\mathbb{N}: \ |x_{n_C}| > C,\nonumber $$ то говорят, что последовательность \eqref{ref6} не ограничена.

Пример 6.

Доказать, что последовательность \(\left\{{\textstyle\frac1{y_n}}\right\}\) является ограниченной, если \(\underset{n\rightarrow\infty}{lim}y_n=b, \ b\neq0, \ y_n\neq0 \ для \ всех \ n\in\mathbb{N}\).

Так как \(b\neq 0\), то \(|b| > 0\). По заданному числу \(\varepsilon=\displaystyle |b|/2\) в силу определения предела последовательности найдется такой номер \(N_0\), что $$\forall n\geq N_0\rightarrow\left|y_n-b\right|<\frac{\left|b\right|}2\label{ref7}$$

Используя данное неравенство, а также неравенство для модуля разности $$\left|b\right|-\left|y_n\right|\leq\left|y_n-b\right|\nonumber$$ получаем \(\left|b\right|-\left|y_n\right|\leq\frac{\left|b\right|}2\), откуда \(\displaystyle \left|y_n\right| > \frac{\left|b\right|}2\), и поэтому для всех n ≥ N, справедливо \(\displaystyle \left|\frac1{y_n}\right|<\frac2{\left|b\right|}\).

Пусть \(C=\displaystyle max(\frac1{\left|y_1\right|},\ldots,\frac1{\left|y_{N_0-1}\right|},\frac2{\left|b\right|})\), тогда для всех \(n\in\mathbb{N}\) выполняется неравенство \(\displaystyle |1/y_n|\leq C\), то есть \(\{1/y_n\}\) — ограниченная последовательность.

Восстановление последовательности документов в 1С

В режиме перепроведения документов в режиме 1С:Предприятие («Главное меню — Все функции — Стандартные — Проведение документов») существует специальная возможность восстановления последовательности проведения документов. При ее использовании система автоматически выполняет перепроведение всех документов, относящихся к данной последовательности, от границы последовательности до указанного момента.

Любое изменение в движениях, допустим, по регистру, на котором ведется стоимостный учет товаров, записанное раньше границы последовательности, будет отодвигать границу последовательности назад, на момент этого документа. После этого проводимые документы, находящиеся позже границы последовательности, уже не будут двигать ее вперед, если между границей последовательности и проводимым документом окажутся проведенные документы из этой последовательности.

После выполнения восстановления последовательности проводимые после границы последовательности документы снова будут двигать границу вперед.

Режим восстановления последовательности позволяет автоматически выполнить перепроведение всех документов, относящихся к последовательности, от текущей позиции границы последовательности до указанного момента. В верхней части диалога следует выбрать позицию, до которой будет выполняться перепроведение документа.

Особенности использования объекта «Последовательность документов»:

1. Основное назначение объекта «Последовательность документов» — автоматизация контроля над хронологическим порядком проведения документов тех видов, которые указаны в последовательности.
2. Объект Последовательность может быть использован с любыми регистрами (можно включить любой регистр, поскольку для любого вида регистра может быть принципиален порядок записей).
3. «Граница последовательности документов» обеспечивает пользователя моментом времени, начиная с которого перепроведение документов последовательности в хронологическом порядке, восстановит правильность (актуальность) учета, контролируемого последовательностью (важен именно момент времени, как комбинация даты (до секунды) и ссылки на конкретный документ внутри этой даты).

4. Чтобы привести учет, контролируемый последовательностью, в актуальное состояние, лучше всего предложить пользователю воспользоваться режимом восстановления последовательности из диалога «Операции» / «Проведение документов…» / «Восстановление последовательностей» (или «Главное меню — Все функции — Стандартные — Проведение документов — Восстановление последовательностей»).

   Рисунок «Восстановление последовательности»

5. Виды документов, которые могут регистрироваться в последовательности документов, указываются в свойстве «Входящие документы» на закладке «Использование» последовательности.

   Пример

   Только документы, указанные в свойстве «Входящие документы», а именно «РасходнаяНакладная», могут регистрироваться в последовательности документов «СебестоимостьПродаж»: Все влияющие на последовательность виды документов указываются явно.

6. Виды документов, которые могут регистрироваться в качестве границы последовательности, должны являться регистраторами регистров, указанных в свойстве «Движения, влияющие на последовательность».

   Пример

   Виды документов, которые могут регистрироваться в качестве границы последовательности «СебестоимостьПродаж»: только документы, являющиеся регистраторами регистров, указанных в свойстве «Движения, влияющие на последовательность», а именно «ПриходнаяНакладная», «РасходнаяНакладная». Приходная накладная, хоть и не включена в последовательность, меняет состояние учета по данному регистру накопления, а значит влияет на границу последовательности.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной. 

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность? 

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N. 

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Сравнение генераторов

Стандартные средства C#

Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом. 

В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности. 

Линейный конгруэнтный генератор (LCG)

Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом. 

При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu. 

Этот генератор страшен тем, что умножает одно большое число на другое и берёт остаток от деления на 231. В результате формируется вот такая красивая картинка. 

XorShift

Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.

Вихрь Мерсенна

Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.

Unity — Random

Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность. 

Перемешанный конгруэнтный генератор (PCG)

Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.

Получить значение AUTO_INCREMENT

LAST_INSERT_ID () является функцией SQL, так что вы можете использовать его из любого клиента, который понимает SQL запросы. В противном случае PERL и PHP скрипты обеспечивают исключительные функции для извлечения автоинкрементного значения последней записи.

Пример PERL

Используйте атрибут mysql_insertid для получения значения AUTO_INCREMENT, генерируемого запроса. Этот атрибут доступен либо через handle базы данных или дескриптор, в зависимости от того, как оформить запрос. Следующий пример ссылается через handle базы данных.

$dbh->do ("INSERT INTO ANDREYEX (name,date,origin)
VALUES('design','2017-04-24','home')");
my $seq = $dbh->{mysql_insertid};

Пример PHP

После выдачи запроса, который генерирует значение AUTO_INCREMENT, получаем значение путем вызова функции mysql_insert_id().

mysql_query ("INSERT INTO ANDREYEX (name,date,origin)
VALUES('design','2017-04-24','home')", $conn_id);
$seq = mysql_insert_id ($conn_id);

Поддержка настройки таблиц последовательности операций бизнес-процесса

Введенные в Dynamics 365 (online) 9.0 таблицы потока бизнес-процессов могут появляться в системе таким образом, чтобы данные строки таблицы можно было сделать доступными в сетках, представлениях, диаграммах и на панелях мониторинга.

С потоками бизнес-процессов, доступными как таблица, теперь можно использовать расширенный поиск, представления, диаграммы и панели мониторинга с источником данных из последовательности операций бизнес-процесса для определенной таблицы, такой как интерес или возможная сделка. Системные администраторы и специалисты по настройке могут создавать настраиваемые сетки, представления, диаграммы и панели мониторинга последовательности операций бизнес-процесса, аналогично созданным с любой другой таблицей.

Последовательности операций бизнес-процесса, например Преобразование интереса в возможную сделку, отображается как настраиваемая таблица в обозревателе решений.

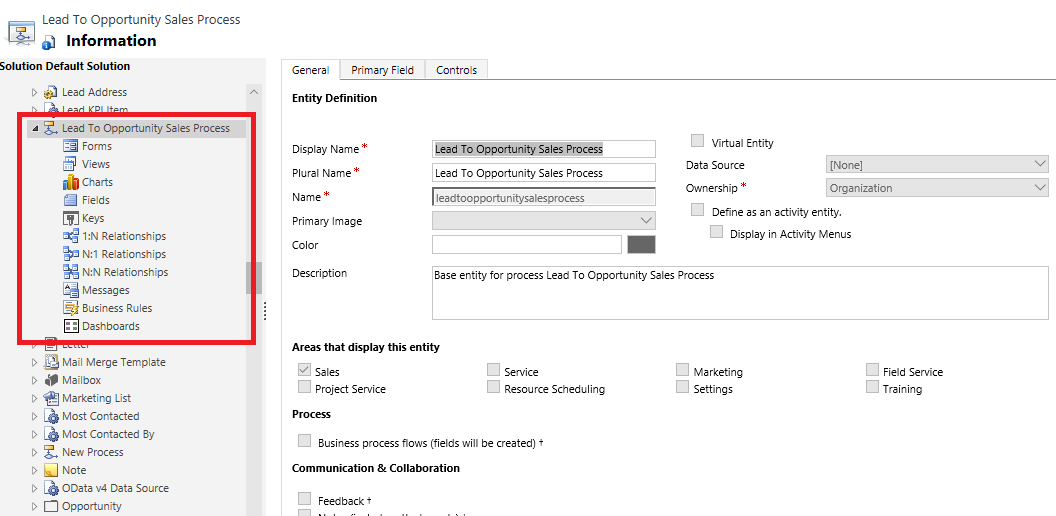
Для получения доступа к представлению последовательности операций бизнес-процесса по умолчанию откройте обозреватель решений, разверните Таблицы > разверните требуемый процесс, например Преобразование интереса в возможную сделку, выберите Представления, затем выберите нужное представление.

Несколько представлений по умолчанию доступны, который можно просмотреть как диаграмму, например представление Активное преобразование возможных сделок в продажи.

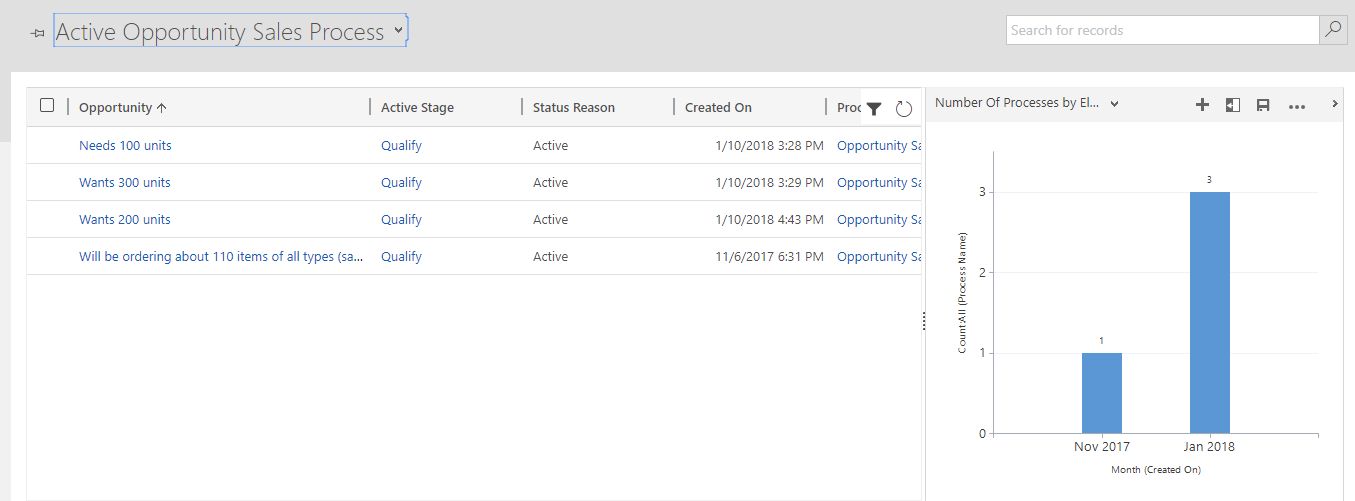
Взаимодействие с таблицей потока бизнес-процессов из рабочего процесса

Вы также можете взаимодействовать с таблицами потока бизнес-процессов из рабочего процесса. Например, можно создать рабочий процесс для строки таблицы «Поток бизнес-процессов», чтобы изменить активный этап при обновлении столбца в строке таблицы «Возможная сделка». Дополнительные сведения о том, как это сделать, см. в записи блога Автоматизация этапов потока бизнес-процессов с помощью рабочих процессов.

Выполнение потоков бизнес-процессов в автономном режиме

Потоки бизнес-процесса можно использовать в автономном режиме, если выполняются приведенные ниже условия.

• Поток бизнес-процессов используется в приложении Power Apps.
• Приложение Power Apps разрешено для использования в автономном режиме.
• Поток бизнес-процесса имеет одну таблицу.

В частности, для потока бизнес-процесса, если приложение Power Apps находится в автономном режиме, доступны три команды:

• Следующий этап
• Предыдущий этап
• Установить активную стадию

Столбец подстановки на этапе поток бизнес-процессов

Последние строки отображаются в столбце подстановки в едином интерфейсе. Чтобы предотвратить отображение в поиске последних использованных элементов, выполните следующие действия:

1. Откройте портал разработчика Power Apps, а затем выберите правильную среду в правом верхнем углу экрана.

2. Перейдите Таблицы в Данные. Найдите таблицу потока бизнес-процессов.

3. Выберите Формы и выберите редактор Информация.

4. Выберите шаг сбора данных поиска в Представление в виде дерева и поставьте флажок Отключить недавно использованные элементы.

5. Сохраните и опубликуйте.

Ограничения использования таблиц потоков бизнес-процесса

• В настоящее время невозможно создать настраиваемые формы для таблиц, основанных на последовательности операций бизнес-процесса.
• Если решение включает в себя таблицу потока бизнес-процессов, ее нужно вручную добавить в решение перед его экспортом. В противном случае таблица потока бизнес-процессов не будет включена в пакет решения. Дополнительные сведения: Создание и изменение таблиц.
• Добавление таблицы процесса в приложение, управляемое моделью, может привести к ограничению функциональности. Узнайте больше о создании и редактировании потоков бизнес-процессов.
• В потоках бизнес-процессов будет отображаться имя экземпляра BPF, которое задается во время создания экземпляра BPF. Это означает, что если имя в определении BPF изменится, в новых экземплярах BPF будет отображаться обновленное имя, а в старых экземплярах BPF —первоначальное имя. Это также означает, что локализованные имена определений BPF не отображаются.

Следующие шаги

Посмотрите короткий видеоролик (4:49) о последовательностях операций бизнес-процессаСоздание последовательности операций бизнес-процессаРасширение потоков бизнес-процессов с помощью ветвления Технический документ. Подготовка процессов в Dynamics 365